CPP Module 02
“CPP Module 02에 대하여”
- POLYMORPHISM in C++
- Orthodox Canonical Class (OCCF)
- ex00: My First Class in Orthodox Canonical Form
- ex01: Towards a more useful fixed-point number class
- ex02: Now we’re talking
Ad-hoc polymorphism, operator overloading and Orthodox Canonical class form
OCCF는 C++의 영원한 친구라고~
POLYMORPHISM in C++
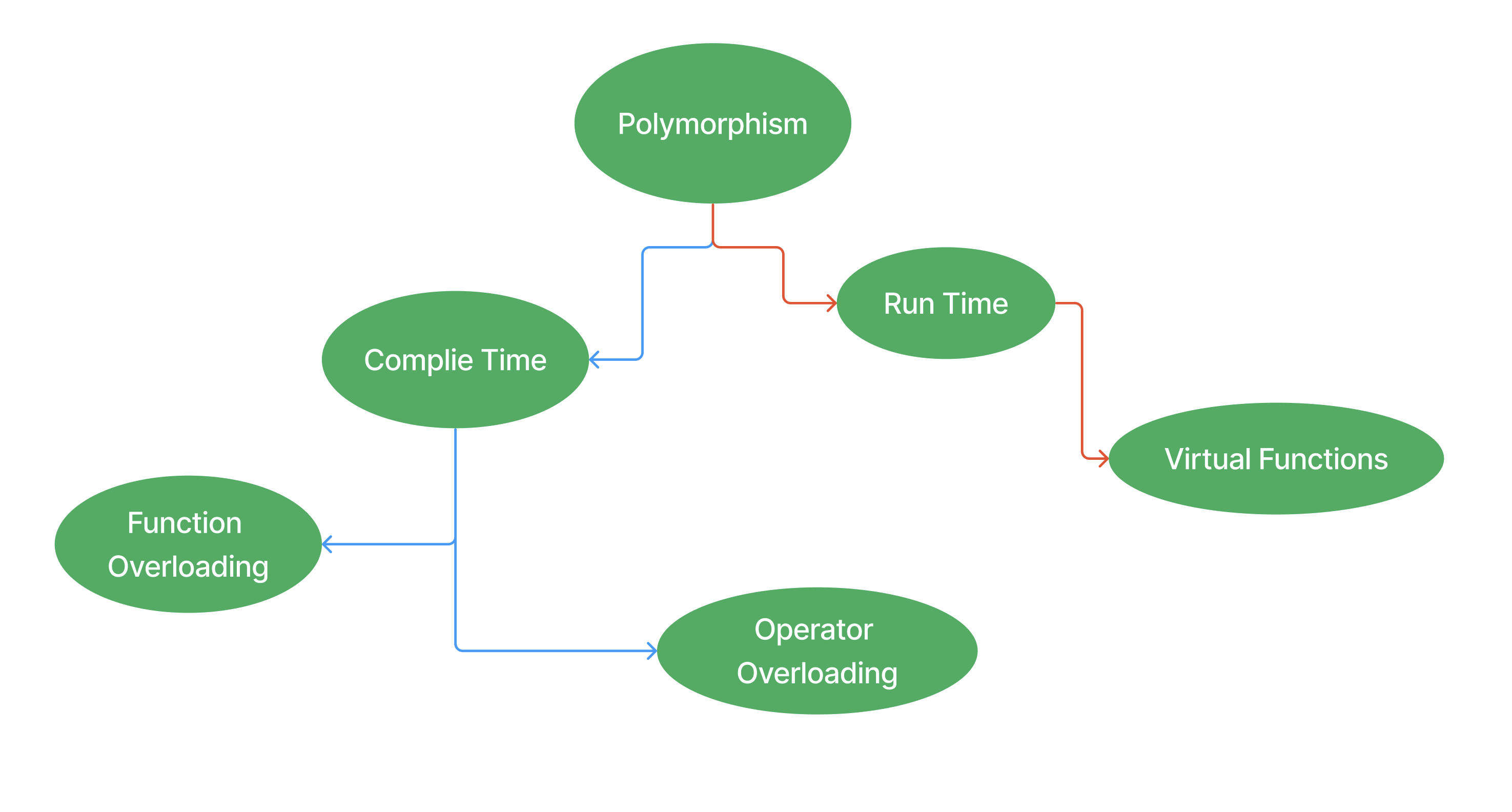
- 다형성(Polymorphism)이란 말 그대로 프로그램 언어의 다양한 요소(상수, 변수, 객체, 함수, 메소드 등등)들이 다양한 데이터에 대해 작동할 수 있는 것을 일컫는 말이다. C++ Polymorphism은 크게 나누었을 때 정적(Static)인 형태와 동적(Dynamic)인 형태가 있다. 이번 과제에서는 주로 정적 다형성에 대해 다루게 될 것이다. 정적 다형성(Static Polymorphism)은 주로 컴파일 타임(Complie Time)에 결정되며, 함수 혹은 연산자 오버로딩(Overloading)과 연관이 있다. (반대로 동적 다형성은 오버라이딩과 관계가 있다).
AD-HOC Polymorphism
- 도대체 C++ 다형성의 종류가 얼마나 되는 것인지 당혹스러울 수 있다. 크게 4개를 알고 있으면 되겠다.
(1) Parametric Polymorphism(Complie Time Polymorphism) : 매개변수 다형성은 동일한 코드를 여러 데이터 유형에 대해 작동하도록 만든다. C++ 템플릿을 이용하여 구현하며, 템플릿을 사용하여 작성한 Generic 코드는 다양한 데이터 유형에 대해 작동할 수 있다. 모듈 07에서 다뤄볼 거다.
(2) Subtype Polymorphism(Runtime Polymorphism) : 서브타입 다형성은 상속과 가상 함수를 통해 생겨나는 다형성이다. 모듈 03, 04에서 다뤄볼 거고 이후에도 계속 등장할 것이다.
(3) Ad Hoc Polymorphism(Overloading Polymorphism) : 임시 다형성은 함수 혹은 연산자 오버로딩을 통해 생겨나며, 이를 통해 함수나 연산자가 다른 데이터 유형에 대해 다른 작동을 하도록 설계할 수 있다. 이번 모듈에서 이야기해볼거고, C++를 하면서 계속 계속 다루게 될 것이다.
(4) Coercion Polymorphism(Casting) : 강제 다형성은 객체 또는 기본 타입이 다른 객체 또는 다른 기본 타입으로 변환할 때 일어난다. Casting은 (unsigned int*)나 (int)와 같이 C 스타일의 타입 캐스팅 표현식을 사용하거나 C++의 static_cast, const_cast, reinterpret_cast, dynamic_cast를 사용할 때 일어난다. 모듈을 불문하고 많은 곳에서 등장한다.
Orthodox Canonical Class (OCCF)
Coplien’s Form 이라고도 한다. (중요)
- 정식 클래스 형식, OCCF는 클래스에 아래 네 가지의 형태를 명시적으로 정의하여 선언하는 것을 가리킨다.
(1) 기본 생성자
(2) 복사 생성자
(3) 할당 연산자 오버로딩
(4) 소멸자
class A
{
A();
A(const A &a);
A &operator= (const A &a);
~A();
};
- 이 형태를 숙지해두면 되겠다. 이제 모듈 끝날 때까지 함께하게 될 것이다.
- 정식 클래스 형식은 연식에 따라 달라지며, C++98 의 OCCF는 위와 같다. C++11에서는 위와 같은 C++98의 정식 클래스 형태에서 &&로 붙는 이동 생성자와, 이동 할당 연산자 2개가 추가된 것이 OCCF라고 한다.
ex00: My First Class in Orthodox Canonical Form
(1) 복사 생성자
class Fixed
{
// ... implementation
public:
Fixed(const Fixed &origin);
// ... implementation
}
int main(void)
{
Fixed a;
Fixed b(a);
// ... implementation
}
💡 복사 생성자는 한 객체의 내용을 다른 객체로 복사하여 생성할 때 사용되는 생성자이다. 복사 생성자는
(1) 자신과 같은 타입의 객체를 인자로 받는다.
(2) 복사 생성자가 정의되어 있지 않다면, 디폴트 복사 생성자가 생성된다. 즉, 클래스 내에 복사 생성자를 정의하지 않더라도 객체 생성 시 컴파일러가 자동으로 복사 생성자를 생성한다.
- 복사 생성자는 매개 변수로 클래스의 참조(Fixed&)를 받는다. 참조로 받지 않으면 복사가 2번 일어나기 때문이다. 또한 const를 붙이는데(const Fixed&), 복사할 개체는 생성자 내에서 값을 직접적으로 변경하지 않기 때문이다.
!주의점!
디폴트 복사 생성자는 “얕은 복사(Shallow copy)”를 수행한다. 즉, 디폴트 복사 생성자에 의해 초기화된 객체는 복사한 객체가 가진 reference와 value 모두 똑같이 가지게 되는 것이다. 따라서 필드에 동적 할당을 받아 초기화되는 변수가 있다면 디폴트 복사 생성자를 이용하지 않고 사용자가 복사 생성자를 직접 정의하여 깊은 복사(Deep copy)가 일어나도록 해야 한다!
클래스 fixed의 복사 생성자는 다음과 같이 작성할 수 있다.
Fixed::Fixed(const Fixed &origin)
{
*this = origin;
}
- 클래스 Fixed의 멤버 함수이므로 Fixed::
- 매개 변수로 상수 참조를 받음 (const fixed &origin)
- this 포인터에 매개 변수의 value를 복사한다.
(2) 할당 연산자 오버로딩
class Fixed
{
// ... implementation
public:
Fixed& operator=(const Fixed &ref);
// ... implementation
}
int main(void)
{
Fixed a;
Fixed b;
b = a; // b.operator = (a)
}
💡 = 연산자는 대입의 우항에 상수 참조(const Fixed &ref)를 받는다. 따라서 우항은 변경되지 않고 좌항만이 변경된다. 반환값은 클래스의 참조로 한다(Fixed &). 이는 operator chaining을 허용하기 위해서이다.
operator chaining
int a, b, c, d, e;
a = b = c = d = e = 42;
- 위와 같이 식을 작성했을 때, 컴파일러는 이를
a = (b = (c = (d = (e = 42))));
와 같이 우측 결합 하여 해석하는데, 이것이 operator chaining이다. 이것이 가능하기 위해 대입 연산자는 반드시 어떤 값을 반환해야 하는데, 그것이 바로 좌항의 참조이다. (Lvalue의 참조)
!주의점!
마찬가지로 대입 연산자 또한 기본적으로 “얕은 복사(Shallow copy)”를 수행한다. 따라서 필드에 동적 할당을 받아 초기화되는 변수가 있다면 대입 연산자를 직접 정의하여 깊은 복사(Deep copy)가 일어나도록 해야 한다! 또한 연산자 내에 동적 할당이 된 경우에는 이전에 동적 할당되었던 데이터를 해제해야 한다. 그렇지 않으면 기존에 있던 데이터가 소멸되지 않아 메모리 누수가 생긴다.
fixed 의 = 연산자 오버로딩 함수는 다음과 같이 작성할 수 있다.
Fixed& Fixed::operator=(const Fixed &ref)
{
std::cout << "Copy Assignment operator called" << std::endl;
if (this != &ref)
{
// ... Copying Values
}
return (*this);
}
- 반환값은 Fixed&
- Fixed 객체 안에 들어있는 멤버 변수임으로 Fixed::
- = 연산자 오버로딩이므로 operator=
- 우항은 변경되지 않고 좌항만 변경되어야 하기 때문에 매개 변수로는 클래스의 상수 참조를 받음. => (const Fixed &ref)
- this는 멤버 함수가 호출되고 있는 오브젝트의 포인터이며, b = a는 b.operator = (a)로 간주할 수 있다. 좌항에는 참조자를 반환해야 하므로 *this를 반환한다.
ex01: Towards a more useful fixed-point number class
[출처] 세계 열강이 경쟁한 19세기, 러시아에게 ‘부동항’이 중요한 이유 #벌거벗은세계사(EP.10, tvN 210313 방송)
… 부동항(不凍港)이라는, 한국과는 일절 상관이 없기에 생소할 법한 이 단어가 우리에게 이렇게나 친숙한 이유는 오직 하나뿐인데, 다름 아닌 러시아가 과거 러시아 제국 때부터 바다로 진출하기 위해서 부동항 확보를 최우선 목표로 하기 때문이다. 조금 과장해서 말하면 부동항을 찾기 위한 여정이 곧 러시아 제국 이후 러시아의 역사였으며, 부동항을 찾기 위한 과정에서 얻은 것이 거대한 시베리아 영토였다 … (나무위키)
- 부동(浮動)소수점은 소수점이 고정되어 있지 않고 부동(浮動)하기 때문에 부동소수점이다. 부가 아닐 부(不)가 아니고 뜰 부(浮)다. 누가 지었는지 몰라도 그냥 꿀밤 500대 맞아야 한다.
부동소수점과 고정소수점
- 42를 이진수로 나타내보라고 하면, 다들 익숙하게 잘 해낼 것이다. 그렇다면 0.4242를 이진수로 나타내본다면 어떨까? 사실 42를 이진수로 나타내기 위해서 2로 나누는 것처럼, 0.4242를 이진수로 나타내기 위해서 2를 곱하면 된다. 대략 아래와 같이 진행될 것이다.
0.4242 * 2 = 0.8484 (정수 부분 0)
0.8484 * 2 = 1.6968 (정수 부분 1), 우항에서 1을 뺀다
0.6968 * 2 = 1.3936 (정수 부분 1), 우항에서 1을 뺀다
0.3936 * 2 = 0.7872 (정수 부분 0)
0.7872 * 2 = 1.5744 (정수 부분 1), 우항에서 1을 뺀다
0.5744 * 2 = 1.1488 (정수 부분 1), 우항에서 1을 뺀다
0.1488 * 2 = 0.2976 (정수 부분 0)
0.2976 * 2 = 0.5952 (정수 부분 0)
...
...
우항의 값이 0이 될 때까지 반복한다. 값은 0.01101100... (2)가 될 수 있다.
아니 우항이 0이 될 때까지 반복한다고요? 그럼 끝이 안 날것 같은데요?
맞다. 끝이 안난다. 다만 자릿수가 길어질수록 더 정밀한 값을 나타낼 거라는 것만은 확실하다. 근데 이 자릿수를 무한정 퍼줄 수가 없다. 아래 그림에 대해 알고 있을 것이다.

- 32비트 기준, 고정 소수점 표기에 관한 그림이다. 저 위에 0.01101100… (2)를 고정 소수점으로 표기한다면 아래 그림처럼 소수점을 기준으로 왼쪽 값이 16의 영역에(정수부, 최대 16개까지), 오른쪽 값이 15의 영역에 차례대로 적히게 될 것이다(소수부, 최대 15개까지). 맨 앞의 부호부는 양수를 가리킨다.

- 딱 봐도 느껴질 것이다. 정수부는 2의 16승까지 나타낼 수 있는데 말 그대로 16칸을 전부 내다버리고 있고, 소수부는 소수부대로 15칸의 정밀도밖에 가져가지 못한다. 0.4242를 표현하는데 정수부는 1칸이면 족한데, 차라리 쓰지도 않는 정수부 칸을 소수부에 줘버려서, 소수부가 더 높은 정밀도를 가질 수 있도록 하면 좋지 않을까?? 라는 생각이 바로 부동소수점이다. 그리고, 이 부동소수를 표현하는 과정에서 소수점이 부동(浮動)하게 된다.
부동소수점 표현하기
- 0.4242를 부동소수로 표현해보자. 2를 곱해서 0.01101100… (2)를 얻어내는 것까지는 동일하다. 다만 이대로 바로 32비트에 16/15로 꽂아넣는게 아니라. 몇 가지 과정을 거치게 된다.
정규화(Normalization)
- 정규화라는 것은 2진수를
1.xxxx... * 2^n
꼴로 변환하는 것을 말한다.
방법은 간단하다. 정수부에 1만 남을 때까지 2를 곱하거나, 나누고, 그 연산을 한 횟수를 n에 기록하면 된다. 위의 0.01101100… (2)를 정규화해보자.
정수부에 1을 오게 만드려면, 2를 2번 곱해서 소수점을 오른쪽으로 2칸 당기면 되겠다. 그러면
1.101100... * 2^-2
와 같은 모양이 나오게 될 것이다. 원래대로 돌리려면 2를 두번 나눠야 하니, n은 -2가 되겠다.
IEEE Standard for Floating-Point Arithmetic
- IEEE 표준에 따르면 부동소수점 방식으로 실수를 저장하는 데는 32비트, 또는 64비트가 사용된다. 32비트는 아래 그림과 같다.

부호부(signed bit) 하나, 지수부(exponent) 8자리, 가수부(fraction/mantissa) 23자리로 이루어져 있다. 23자리 가수부에 정규화 결과 소수점 오른쪽에 있는 숫자들을 왼쪽부터 그대로 꽂아넣으면 된다. 남는 자리는 0으로 채운다. (왼쪽에 있는 1은 어차피 1이기 때문에 표현하지 않는다. 이 1을 hidden bit라고도 한다.)
나머지 지수부에는 n의 값을 집어넣으면 되는데, 이 값을 그대로 넣는게 아니라 bias라 부르는 어떤 수를 더해서 넣어줘야 한다. 이 편차값은 n이 음수일 때를 대비하여 생긴 값이다. n이 음수면 저장하기가 곤란하기 때문이다. 32비트 기준으로 bias 값은 127이다. -4 + 127, 즉 123을 지수부에 저장한다. 지수부에 저장되는 값이 0 ~ 127이라면 n이 음수, 128 ~ 255라면 n이 양수라는 것을 알 수가 있다.(0이나 255는 일반적인 표현 범위에는 포함되지 않고, nan이나 inf와 같은 것들을 표현하기 위해 남겨놓는다고 한다.)
0.4242를 부동소수로 나타낸 결과는 아래와 같다. 지수부에는 123이, 가수부에는 정규화 결과, 소수점 오른쪽에 있던 23개의 값이 들어가 있다.

위 그림의 32비트 표기를 32비트 단정도(Single-Precision), 64비트 표기를 64비트 배정도(Double-Precision)라고 부른다. 32비트가 float, 64비트가 double이라고 생각하면 되겠다.
64비트 배정도에서는 지수부가 11비트, 가수부가 52비트다. 지수부가 2^11이므로(2048), 0~1023 구간은 음수, 1024~2047 구간은 양수 지수를 의미하며 bias는 1023이다.

부동소수점의 오차
- 부동 소수점 방식을 사용하면 고정 소수점 방식보다 더 많은 범위까지 표현하면서도 정밀도를 높일 수 있기 때문에, 대부분의 컴퓨터 시스템이 부동소수점을 사용한다고 한다. 물론 부동소수점에도 오차가 존재한다. 이진수로 변환하는 과정에서 생기는 오차를 근본적으로 없앨 수는 없기 때문이다. 이는 C++를 포함한 모든 컴퓨터 프로그래밍 언어에서 발생하는 문제이기도 하다. 자신이 사용하는 코드 에디터에서 다음과 같은 표기를 본 적이 있을 것이다. VS code 기준 아래와 같다.

(double)(0.1000000000000000056)의 경우 소수점 19자리까지 표현된 것으로, 이는 상당히 높은 정밀도다. 이것이 가능한 비결이 바로 가수부(Mantissa)에 52자리를 확보할 수 있는 64비트 배정도에 있다. 다른 소수들도 마찬가지다. 저 코드… 무엇을 출력할까?
❯ ./a.out
0%
- 당근 0을 출력하겠다. 0.1도 0.1이 아니니, 0.2도 0.2가 아닐 거고 0.1에 2를 곱한 것도 0.2가 아니고 … 점점 오차의 늪으로 빠져들게 된다.
부동소수점을 8비트 고정소수점으로 나타내기
- 앞에서 부동소수점, 고정소수점 이야기를 길게 했는데, 결국 이번 과제의 컨셉트는 부동소수를 8비트 고정소수로 나타내는 것에 있다. 42.42를 8비트 고정소수로 바꿔보자.

- 42.42 자체가 VS code에 부동소수로 저장되어 있기 때문에(42.4199981689453125 …), 별다른 준비작업 없이 바로 시작하면 된다. 대략적인 과정은 아래와 같다.
(1) 부동소수에 256를 곱함(생성할 때, float 생성자)
(2) 반올림을 한다 (roundf)
(3) 그 후 256를 나눈다(출력할 때, toFloat)
- 바꾸는 건 생각보다 간단한데, 조금 들여다보자면 아래와 같다. 소수점을 가리키는 화살표에 주목하자.
(1) 42.42(42.4199981689453125)를 이진수로 나타낸다.
↓ (소수점)
=> 101010.0110 1011 10000101000111101011100001010001111011 (2)
(2) 여기에 256을 곱한다 (부동 소수는 비트 쉬프팅이 불가능)
(3) 소수부에서 8자리가 밀려 올라오게 된다. (2의 8승을 곱했으니까)
↓ (8칸 밀린 소수점)
=> 101010 0110 1011.10000101000111101011100001010001111011 (2)
= 10859.52(10859.51953125)
(4) 반올림하면서 남은 소수부를 전부 버린다. 소수점 부분이 전부 잘려나가게 된다.
=> 101010 0110 1011. (화살표 뒷부분이 전부 잘려나간다)
= 10860
(5) 다시 256을 나눈다
↓
=> 101010.0110 1100 (2)
= 42.421875
⇒ 소수부가 8자리인 고정 소수로 나타내기!!
⇒ float의 정밀도는 6, 따라서 42.4219로 표기!!
- 결국 8비트 고정소수로 만든다는게, 8비트 빼고 싹다 반올림해서 버려버린다는 거다. 버려지는 만큼 오차가 생기는 건 어쩔 수 없는 부분이다. 42.4199981689453125… 가 42.421875로 8비트로 줄었고, float 정밀도인 6에 맞춰서 42.4219가 되어버렸다.
ex02: Now we’re talking
6개의 비교 연산자, 4개의 산술 연산자, 그리고 4개의 증감 연산자(전위 증가/후위 증가/전위 감소/후위 감소) 오버로딩 함수를 구현해야 한다.
그리고 4개의 public 오버로딩된 멤버 함수를 추가한다.
(1) 여태까지 만들어놓은 fixed-point numbers 클래스의 참조 2개를 매개변수로 받아서, 둘 중 작은 것의 참조를 반환하는 static member function min.
(2) fixed-point numbers 클래스의 상수 참조 2개를 매개변수로 받아서, 둘 중 작은 것의 참조를 반환하는 static member function min.
(3) fixed-point numbers 클래스의 참조 2개를 매개변수로 받아서, 둘 중 큰 것의 참조를 반환하는 static member function max.
(4) fixed-point numbers 클래스의 상수 참조 2개를 매개변수로 받아서, 둘 중 큰 것의 참조를 반환하는 static member function max.
비교 연산자의 경우, 두 Fixed를 비교해서 적당한 bool을 반환하면 되고, 산술 연산자의 경우 두 Fixed를 연산해서 알맞은 Fixed를 내놓으면 되는 비교적 간단한 오버로딩 함수들이지만, 전위/후위 증감 연산 오버로딩 함수의 경우 알아야 할 부분이 좀 있다.
L-value & R-value
a = 42;
// ... a를 이용한 연산들
예를 들어, a는 L-value, 42는 R-value이다.
L-value와 R-value에 대해 자세하게 알고 싶다면, 아래 링크 참고
콕 집어말하자면, L-value는 객체를 참조하는 표현식이다(메모리 위치를 가지고 있다).
C++ 표준은 R-value를 정의할때, 제외 개념으로 처리하고 있는데, 다음과 같다. “모든 표현식은 L-value 거나 R-value이다” 고로, R-value 는 L-value 가 아닌 모든것이다. 정확하게 말하자면, 구분 가능한 메모리 영역을 가지는 객체를 나타낼 필요가 없는 표현식이다(임시로 존재하는 것일 수 있다).
후위 증가 연산자 표현식의 결과는 R-value이다.
int a = 42;
- a는 스택 메모리에 위치하는 L-value이다. a는 해제되기 전까지 메모리를 참조하거나, 변경할 수 있다.
a++;
- 위 표현식의 결과는 R-value이다. 객체 a의 값을 복사하여 변경한 후, 임시 복사를 반환하기 때문이다.
a++ = 43; // Compile Error
main.cpp:7:6: error: expression is not assignable
a++ = 43;
표현식의 결과가 R-value라는 것은, 위의 식이 성립하지 않는 것으로 증명된다. 임시값에 어떠한 값을 할당할 수 없다.
반대로 아래는 성립한다. 전위 증가 연산자 표현식의 결과는 L-value이다. L-value에는 값을 할당할 수 있다.
#include <iostream>
int main()
{
int a = 42;
++a = 4242; // Assignment in L-value, OK
std::cout << a; // 4242
}
❯ ./a.out
4242%
- 정리하자면, 우리가 표현식의 주소를 얻을 수 있다면 그것은 L-value 표현식이고 그렇지 않다면 R-value 표현식이다. 그리고 우리가 구현할 전위/후위 증감 연산자 오버로딩 함수 또한 이 규칙을 따른다.
전위 증감 연산자
Fixed& Fixed::operator++() // Pre increment
{
this->fixed++;
return (*this);
}
Fixed& Fixed::operator--() // Pre decrement;
{
this->fixed--;
return (*this);
}
- 결과가 L-value인 전위 증감 연산자이다. 연산이 실행되는 그 라인 단계에서 이미 증감 연산이 적용되어 있으며, 그 값을 변경할 수도 있다. 값을 더하거나 빼서, 곧바로 그 참조를 반환한다. 매개 변수를 빈 칸으로 남겨놓는데, 이를 통해 후위 증감 연산자와 구분할 수 있다.
int a = 42
std::cout << ++a << std::endl; // pre increment, (a = 42 + ϵ) > 42
++a = 4242; // Assignment in L-value, OK
후위 증감 연산자
const Fixed Fixed::operator++(int) // Post increment
{
const Fixed ret(*this); // copy value
this->fixed++;
return (ret); // disappear after line
}
const Fixed Fixed::operator--(int) // Post decrement
{
const Fixed ret(*this);
this->fixed--;
return (ret); // disappear after line
}
- 결과가 R-value인 후위 증감 연산자이다. 연산이 실행되는 라인 단계에서는 연산이 적용되어 있지 않고, 값을 변경할 수도 없다. 먼저 임시 복사값을 생성한 후, 원본 값에 연산을 실행하고 임시 복사값을 반환한다. 이 임시 복사값은 라인이 끝나고 나면 사라진다(R-value).
Fixed a(42);
std::cout << a++ << std::endl; // post increment, a = 42
std::cout << a << std::endl; // (a = 42 + ϵ) > 42
a++ = 4242; // Assignment in R-value, Error
- 임시 복사값이 라인이 끝나고 나면 사라진다는 말은,
std::cout << a++ << std::endl;라인이 실행되면서 반환된 값 ret가, “;”으로 해당 라인이 끝나고 그 다음 라인(std::cout << a << std::endl;)으로 넘어가는 순간 사라져버린다는 것이다. 다음 라인에서는 ret은 사라지고 연산이 적용된 원본 값의 value가 출력된다(42 + ϵ / 42 - ϵ).
왜 ++a++는 안될까?
⇒ 연산자 우선순위에 따라 ++a++는 ++(a++)가 된다. a++는 Rvalue이므로 증감 연산의 피연산자가 될 수 없기 때문에 오류가 발생한다. (++a)++는 가능, ++a는 Lvalue이기 때문에 증감 연산 피연산자가 될 수 있다.
왜 후위 연산 오버로딩은 const로 반환할까?
⇒ 살펴보았듯이 (a++)++은 첫 후위 연산의 반환값이 Rvalue이기 때문에 그 다음 후위 연산이 불가능하다. 즉 C++은 후위 증가의 연속 표현을 배제하기 때문에 오버로딩하는 함수 또한 연속적인 후위 연산을 배제해야 하며, 후위 연산의 반환값을 const로 반환해서 값을 변동할 수 없도록 만들어 연속적인 후위 연산을 막는 것이다.
