CPP Module 09

21 Dec 2023 in 42Cursus on CPP Module

“CPP Module 09에 대하여”

• ex00: Bitcoin Exchange
  • 개요
  • 문자열 스트림, std::stringstream
  • 없는 날짜 고르기
  • data.csv 파싱에 관하여
• ex01: Reverse Polish Notation
• ex02: PmergeMe
  • 대략적인 과정
    • 이진 탐색 수 줄이기
  • vector와 deque의 std::swap 차이점
    • std::vector, 그냥 우리가 아는대로 vec[i], vec[i + 1]이 바뀜
    • std::deque, deque a와 deque b간의 swap이 일어남
  • std::vector, std::deque, std::list 비교
    
    • (1) std::vector
      • * 장점
      • * 단점
    • (2) std::deque
      • * 특징
      • * 주의
    • (3) std::list
      • * 특징
      • * 단점 & 주의
  • 결론

STL

이제 당신도 c++ 잘알

ex00: Bitcoin Exchange

김해 제육 청년 김찬호 선생님 화이팅!!

개요

• 특정 일자의 비트 코인 가격을 출력하는 프로그램을 만들어야 한다.

• 프로그램은 비트 코인의 일자별 가격이 적혀 있는 .csv 파일로 주어지는 데이터 베이스를 사용해야 한다. 이 데이터베이스는 서브젝트에서 제공된다.

• 프로그램은 input 파일로 두 번째 데이터 베이스를 받는데, 그 데이터 베이스 안에는 평가할 일자와 가격이 제시되어 있다.

---

프로그램이 따라야 할 규칙이 있다

(1) 프로그램 이름은 btc여야 한다.

(2) 파일을 인자로 받아야 한다.

(3) 그 파일은 “date | value” 의 형식으로 이루어져 있어야 한다.

(4) 적절한 일자는 언제나 “Year-Month-Day” 의 형식을 따라야 한다.

(5) 적절한 value는 0과 1000 사이의 float 혹은 양의 정수이다.

• 이번 모듈에서 각 exercise를 진행할 때, 최소한 하나의 컨테이너(STL Container)를 사용해야만 한다. 또한 발생할 수 있는 에러에 대해 적절한 메세지를 출력해야만 한다.

---

• 서브젝트에서 프로그램이 받을 두 번째 데이터 베이스 input.txt의 예시를 보여준다. 아래와 같다.

$> head input.txt
date | value
2011-01-03 | 3
2011-01-03 | 2
2011-01-03 | 1
2011-01-03 | 1.2
2011-01-09 | 1
2012-01-11 | -1
2001-42-42
2012-01-11 | 1
2012-01-11 | 2147483648
$

• “date | value” 로 구성되어 있는 모습, value는 들쑥날쑥한데, 적절한 예외 처리를 해야 할 것이다.

• 프로그램은 input.txt의 일자에 맞는 Bitcoin의 value에, data.csv에 주어진 일자에 맞는 Bitcoin의 exchange rate를 곱한 값을 표준 출력 해야 한다. 이 또한 서브젝트에 예시가 주어져 있다.

$> ./btc
Error: could not open file.
$> ./btc input.txt
2011-01-03 => 3 = 0.9
2011-01-03 => 2 = 0.6
2011-01-03 => 1 = 0.3
2011-01-03 => 1.2 = 0.36
2011-01-09 => 1 = 0.32
Error: not a positive number.
Error: bad input => 2001-42-42
2012-01-11 => 1 = 7.1
Error: too large a number.
$>

• 만약 input.txt에 주어져 있는 날짜가 data.csv에 없다면, input.txt의 날짜와 가장 가까운 날을 고르되, input.txt의 날짜를 넘지는 말아야 한다. 이건 예시를 보면 알 수가 있다. 당장 data.csv에 2011년 1월 3일의 비트 코인 exchange rate는 주어져 있지 않은데, input.txt를 보면 2011년 1월 3일에 3개의 bitcoin value가 주어져 있다. data.csv에서 11년 1월 3일과 가장 가까운 날인데, 11년 1월 3일을 넘지 않는 날짜는 11년 1월 1일인데 data.csv에 책정된 11년 1월 1일의 bitcoin exchange rate는 0.3이다. 그래서 3과 0.3을 곱한 0.9를 출력한다. 나머지도 마찬가지다. input.txt의 11년 1월 9일도 data.csv에는 없어서, 적절한 날짜인 11년 1월 7일의 rate를 value에 곱해 출력한다(0.32). 그 외의 에러는 따로 메세지를 출력한다.

• 이게 프로그램 구동 예시 위에 The following is an example of the program’s use 라는 말이 써져 있어서 그냥 예시 정도로 생각해도 될 법한데, 사실 이것 그대로 구현하는게 마음이 편하다. 본인은 처음에 이 예시를 유심히 보지 않고 Error가 발생했을 때 exception을 던져서 그 즉시 프로그램을 return하도록 짰는데, 출력이 이 예시랑 너무 달라져서 한번 갈아엎었었다.

이번 ex에서 사용한 STL Container는 이후 ex들에서는 사용할 수 없다!

문자열 스트림, std::stringstream

• 이번 모듈 전체를 관통하는 주제인 문자열 스트림이다. cpp module은 c++98만을 사용하도록 제한되어 있어, 문자열 파싱에 유용한 c++11의 스트링 변환 함수(stoi, stof, stod)를 사용할 수가 없다(단, c 함수인 std::strtod는 사용할 수 있다). 따라서 직접 스트림 변환을 해줘야 한다. 예시 코드를 살펴보자.

#include <iostream>
#include <sstream>
#include <string>
using namespace std;

int main() 
{
    stringstream iss("test 123 aaa 456");

    string s1, s2;
    int i1, i2;

    iss >> s1 >> i1 >> s2 >> i2; 
    // 공백 혹은 개행을 기준으로 문자열을 parsing하고, 변수 형식에 맞게 변환

    cout << s1 << ' ' << i1 << ' ' << s2 << ' ' << i2 << endl;

	cout << sizeof(s1) << ' ' << sizeof(i1) \
		<< ' ' << sizeof(s2) << ' ' << sizeof(i2) << endl;
}

❯ ./a.out
test 123 aaa 456
24 4 24 4

• istringstream iss를 선언하고 string인 test 123 aaa 456으로 초기화했다. stringstream은 문자열을 마치 스트림처럼 다룰 수 있도록 해주기 때문에, iss를 통해 파일에서 스트림(cin, getline 등)으로 입력받는 것 처럼 string의 내용을 입력받을 수 있도록 만들어준다. 뿐만 아니라 입력받을 때 변수의 자료형을 정해주면, 그 형식에 맞도록 자동으로 변환된다. 이는 상당히 강력한 기능이다.

• 위 코드에서 s1, s2는 string, i1, i2는 int로 선언되었고, stringstream으로 문자열 변환을 마친 후 각 변수의 size를 출력하면 형식에 맞게 변환되어있다는 사실을 알 수가 있다. 스트림 변환을 통해 data.csv와 input.txt를 편리하게 파싱할 수 있다.

없는 날짜 고르기

• input.txt의 날짜가 data.csv에 존재하지 않는다면, 가장 가까우면서도 그 input.txt의 날짜를 넘지 않는 data.csv의 날짜를 꼽아서 그 exchange rate에 input.txt의 value를 곱해서 출력해야 한다. 이는 std::lower_bound()를 통해 구현할 수가 있다. 알고리즘 문제를 풀면서 이분 탐색에 대해 공부한 적이 있다면 익숙한 함수일 것이다. std::lower_bound와 std::upper_bound에 대해 공부해보려면 아래 링크 참조

(1) 모두의 코드, C++ 레퍼런스 - std::lower_bound 와 upper_bound (algorithm)

• lower_bound와 upper_bound는 lower와 upper라는 단어 때문에 마치 찾으려는 값이 컨테이너에 존재하지 않는다면 각각 찾으려는 값에 가장 근접하면서 작은 요소의 반복자, 가장 근접하면서 큰 요소의 반복자를 반환할 것 같은 착각을 일으키지만 lower_bound는 찾으려는 값보다 같거나 큰 값의 반복자를 반환하고, upper_bound는 찾으려는 값을 처음 초과하는 지점의 반복자를 반환한다. 따라서 문제의 의도대로 날짜를 찾기 위해서는 lower_bound를 사용하여 날짜와 가장 가까운 다음 날의 날짜를 찾은 후, 반복자를 하나 빼서 찾으려는 날짜보다 이전의 날짜로 조정해야 한다. 또, input의 날짜가 data.csv의 날짜보다 너무 이르거나 너무 멀거나 해서 생기는 오류들도 따로 처리해야 한다.

data.csv 파싱에 관하여

• 과제를 구현하면서 생각해봤던 이슈다. data.csv는 대략

date,exchange_rate
2009-01-02,0
2009-01-05,0
2009-01-08,0
2009-01-11,0
2009-01-14,0
2009-01-17,0
...

• 이런 형식으로 이루어져 있는데, 이걸 파싱해야하냐 말아야하냐는 거다. 본인은 파싱하긴 했다. “.csv” 같은 파일 확장자 뿐만 아니라, 라인별로 파싱을 해줬다. 그런데 data.csv를 파싱한다는 것은 평가자가 data.csv의 확장자를 바꾸는 것 이외에 data.csv를 변조한다는 것을 전제하는 건데, 평가하는 과정에서 그 정도까지의 검증이 필요하지 않다고 생각하기 때문에 data.csv를 파싱하는 것에 대해 의문을 가지게 되었다. 물론 input.txt를 파싱했다면 그 로직을 그대로 가져오면 되기 때문에, data.csv를 파싱하는 것 자체는 어렵지 않다. 연습삼아 해보는 것도 나쁘지 않을지도…

ex01: Reverse Polish Notation

• 후위 표기법을 구현해보는 과제이다. 태생이 문과인 나는 접해본 적이 없는 계산법이지만, 대략 컴퓨터가 연산을 쉽게 하도록 표현하는 방법이라고 한다. 우리가 평소에 사용하는 중위 표기법과 달라 이질적이지만, 알고리즘을 통해 스택 문제들을 접해보았다면 아주 낯설지는 않을 것 같다.

• 마찬가지로 stringstream을 기깔나게 쓸 수 있는 문제이다. stringstream과 strtod를 사용하면 손쉽게 수식을 double과 operator로 파싱할 수 있다.

• 수식을 파싱하여 숫자라면 스택에 추가하고, 연산자라면 스택에서 숫자를 제거하여 해당 연산을 수행한 이후 다시 스택에 넣는다. 모든 연산이 끝난 후에는 스택에 최종적인 연산의 결과값만이 남아있어야 한다. 또 연산자 하나에 스택의 top의 원소와 그 아래 숫자의 연산이 실행되고 그 결과값이 다시 스택에 push되기 때문에, 숫자의 개수는 연산자의 개수보다 항상 하나가 많아야 한다. 이것을 체크하기 위해 연산자가 들어왔을 때 최소한 스택의 숫자가 2개 들어있는지, 모든 연산이 실행되었을 때 스택의 size가 1인지 등을 체크해야 할 것이다.

• 알고리즘 문제를 푸는 것 같아서 흥미로운 exercise였다. 또 괄호를 구현할 필요가 없어서 난이도가 아주 높지는 않았다. 괄호를 구현해야했다면 더 까다로운 exercise가 되었을 것이다.

ex02: PmergeMe

• 양의 정수 시퀀스 컨테이너를 매개 변수로 받아서, 병합-삽입 정렬을 사용하여 정렬하는 프로그램 PmergeMe를 구현해야 한다.

• 꼭 집어 말하자면, 포드-존슨 알고리즘을 사용해야 한다.

• 이 exercise는 push_swap과 비슷한 점이 있는데, push_swap은 어떻게든 명령어의 개수를 최소화하는 것이 목표고, 포드-존슨 알고리즘은 이진 탐색의 수를 최소화하는 것이 목표라는 점이다. 단도직입적으로 결론부터 말하자면 Jacobstahl수 순서대로 이진 탐색을 시도함으로써 확률적으로 이진 탐색의 숫자를 줄일 수 있다. 대략적인 과정을 보여주면서 부연 설명을 붙이도록 하겠다.

---

!주의!

• 본인은 이 exercise에서 재귀를 사용하지 않았다. 본인이 과제를 진행할 때는 잘 몰랐던 사실인데, 들어보니 포드-존슨 알고리즘은 재귀를 사용하는 알고리즘이라고 한다. 생각해보면 포드-존슨 알고리즘은 결국 병합-삽입 정렬인데, 병합 정렬 자체가 재귀를 기반으로 한다는 걸 생각해보면 당연한 게 아닌가 싶기도 하다. 만약 포드-존슨 알고리즘을 진짜 제대로 구현하고자 한다면, 재귀를 사용해서 배열을 나눈 후 이진 탐색으로 삽입하는 과정을 거쳐야 할 것이다. 내꺼따라하다가fail받을수있다는뜻

---

대략적인 과정

• 엉성한 구현이기는 하지만, 본인이 과제를 해결한 대략적인 절차를 설명하면서 모듈 9를 마무리하도록 하겠다. 예시로 정렬할 배열은 {21, 15, 34, 56, 41, 44}이다.

(1) 매개 변수로 배열을 받아 배열이 모두 양의 정수로 이루어져 있는지 검사하고, 만약 그렇다면 Jacobsthal 수로 이루어져 있는 배열을 만든다. Jacobstahl수로 이루어진 배열의 size는 매개변수로 주어진 배열의 size와 동일하게 맞췄다. 그러면 Jacobstahl 수가 무조건 매개변수로 주어진 배열의 size를 넘게 된다.

void	PmergeMe::fillJacobsthal()
{
	int	limit = vec.size(); // 매개 변수로 주어진 배열을 파싱한 vector
	int idx = 0;
	int	cur = 1; // Jacobstahl 수, 1을 push하고 계산 시작

	while (cur <= limit)
	{
		vecJacobsthal.push_back(cur);
		idx++;
		int next = pow(2, idx + 1) - vecJacobsthal[idx - 1]; // 주요 로직
		cur = next;
	}

	std::deque<int> deq(vecJacobsthal.begin(), vecJacobsthal.end());
    // deq 전용 Jacobstahl 배열을 따로 썼다. 지금보니 좀 비효율적인 것 같기도...
	deqJacobsthal = deq;
}

• Jacobstahl수의 배열을 채우는 함수다. 수식을 생각해내는게 꽤 까다로웠던 기억이 난다.
  

(2) 배열이 {21, 15, 52, 56, 33, 44}와 같을 때, 한 쌍을 묶어서 {큰 값, 작은 값}이 오도록 정렬한다({(21, 15), (56, 52), (44, 33)}). 이후 큰 값을 기준으로 오름차순으로 정렬한다. 즉 큰 값만을 추렸을 때, 오름차순이어야 한다. 즉 {(21, 15), (44, 33), (56, 52)}이 되도록 정렬한다.

• 이전

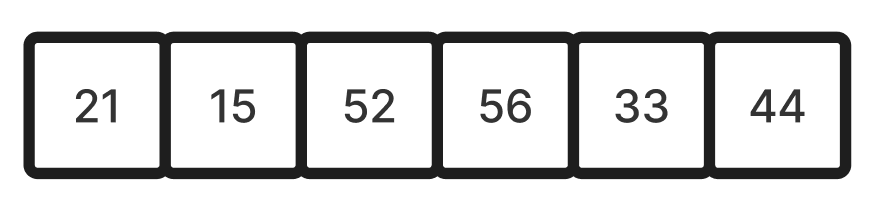
• 이후

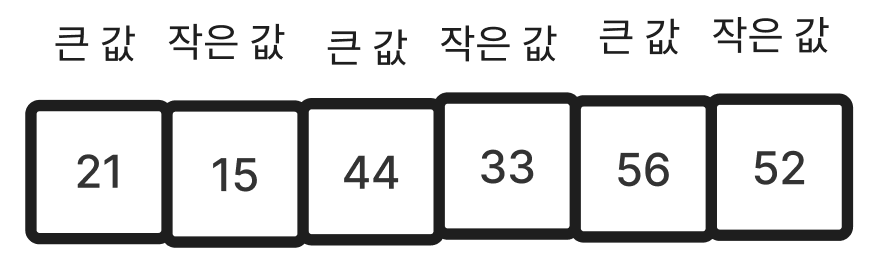
(3) 배열을 두 개로 나눈다. 하나는 바로 위 사진에서 “작은 값” 만으로 이루어진 배열이고, 나머지는 “큰 값” 만으로 이루어진 배열이다. 여기까지가 “병합-삽입” 중의 “병합”이다. 이후의 작업은 삽입이다. (배열이 홀수 개라면 나머지 하나는 그냥 작은 값 배열의 끄트머리에 넣어버린다). std::pair를 통해 편하게 진행할 수 있다.

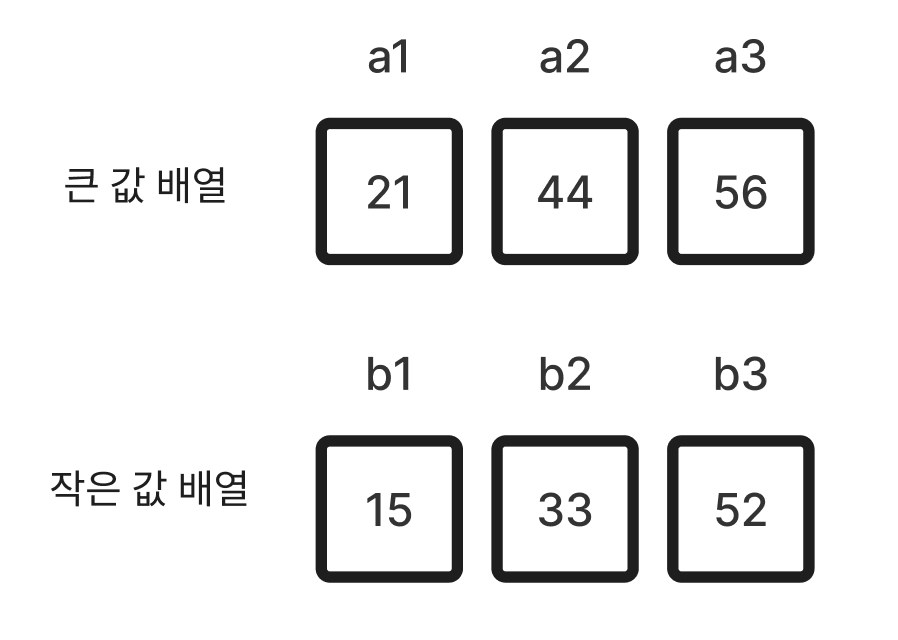
진짜 제대로 된 포드-존슨 알고리즘이라면 여기까지의 과정이 재귀로 이루어져 한다는 것으로 생각하고 있다. 병합 정렬을 하듯이 배열을 둘로 나누어 더 이상 나눌 수 없을 때까지 나눈 후, 배열을 합치면서 이렇게 배열을 둘로 나누면 되지 않을까? 하고 생각한다. 생각만해본다해보고싶진않다

(4) 이제 작은 값 배열의 숫자를 큰 값 배열에 삽입하면서 정렬한다. 이때 순서대로 집어넣는게 아니라 Jacobstahl수를 따르면서 삽입한다. 이때를 위해 만들어둔 Jacobstahl수 배열을 꺼내온다. 지금 정렬하려는 배열 size가 6이라서 준비된 Jacobstahl 배열도 size가 6인데, 배열이 길어지면 Jacobstahl 배열 또한 그 size에 맞춰지도록 설정했다.

Jacobstahl수를 따르면서 삽입한다는 건, 15(1) 33(2) 52(3) 순서대로 큰 값 배열에 집어넣는게 아니라 Jacobstahl수를 따라서 15(1) 52(3) 33(2) 순서로 큰 값 배열에 집어넣는다는 것이다. 만약 매개변수로 주어진 배열이 6개보다 더 길다면, 1 3 2 5 4 11 10 9 8 7 6 … 과 같은 순서로 삽입한다.

(4 - 1) 15를 넣는다. (b1)

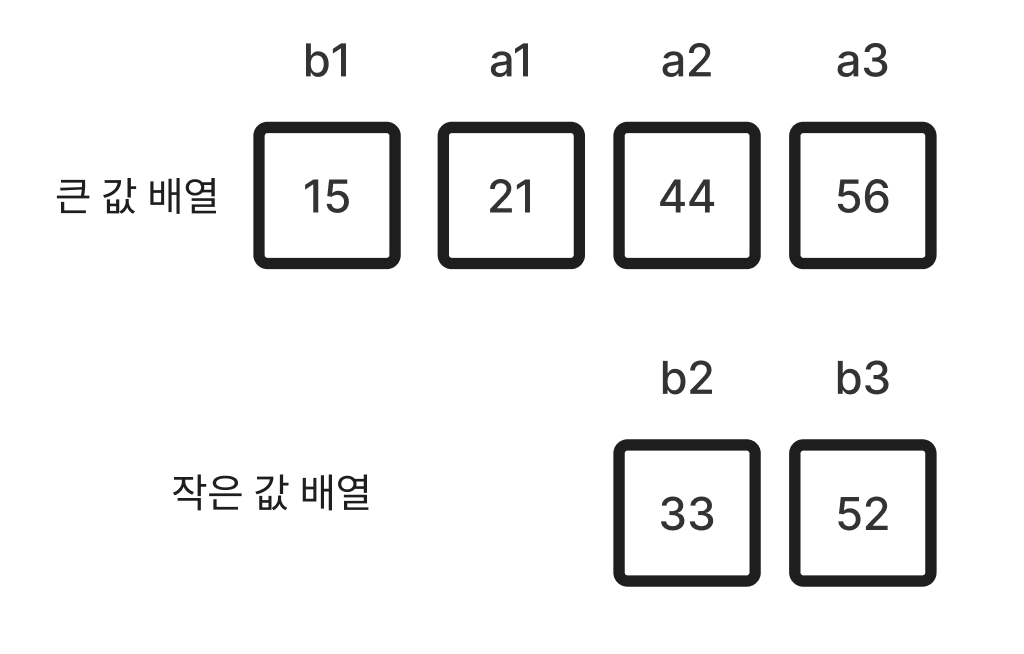
(4 - 2) 52를 넣는다. (b3)

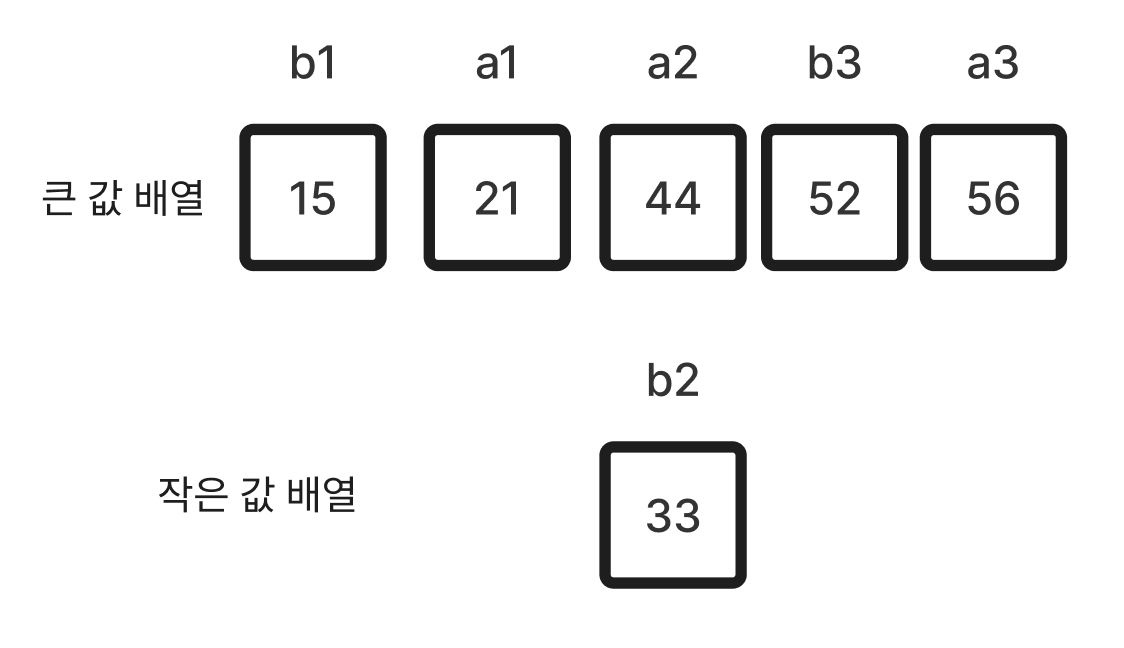
(4 - 3) 33을 넣는다. (b2) -> 정렬 끝

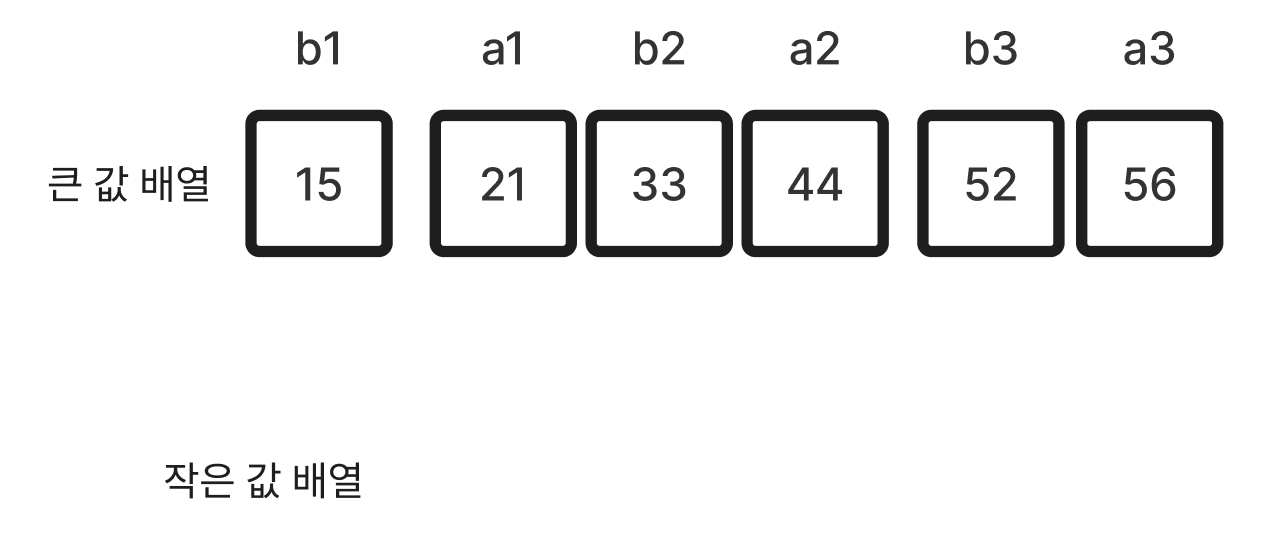
이진 탐색 수 줄이기

• 결국 위 과정은 이진 탐색 수를 최대한 줄여가면서 b 배열에서 a 배열에 수를 집어넣기 위한 세팅이다. 이진 탐색 수가 줄어든다는 것을 이해하기 위해서는 이진 탐색 수를 계산하는 매커니즘을 알아야 한다. 이진 탐색 수는 정렬할 수 있는 경우의 수가 2의 제곱수일때마다 늘어나게 된다.(2, 4, 8 …) 이진 탐색 수를 줄이기 위해서는 정렬할 수 있는 경우의 수를 줄이는 것이 핵심이다.

(경우의 수 1, 2개 -> 이진 탐색 수 최대 1번으로 자리 찾기 가능)
(경우의 수 3, 4개 -> 이진 탐색 수 최대 2번으로 자리 찾기 가능)
(경우의 수 5, 6, 7, 8개 -> 이진 탐색 수 최대 3번으로 자리 찾기 가능)
...

(5) 삽입할 때, 삽입 정렬처럼 반복문을 도는게 아니라 이진 탐색을 실행한다. 큰 값 배열은 언제나 오름차순으로 정렬되어 있기 때문에 별도의 절차 없이 바로 이진 탐색을 실행하면 된다(큰 값 배열은 정렬되어 있지 않다). 이때 Jacobstahl 수 순서대로 정렬하면 이진 탐색의 수를 줄일 수 있다. 줄일 수도 있다는 게 포인트다, 무조건 줄어드는 게 아니다. 직접 경우의 수를 확인해보자.

(5 - 1) Jacobstahl 순서를 따르는 경우

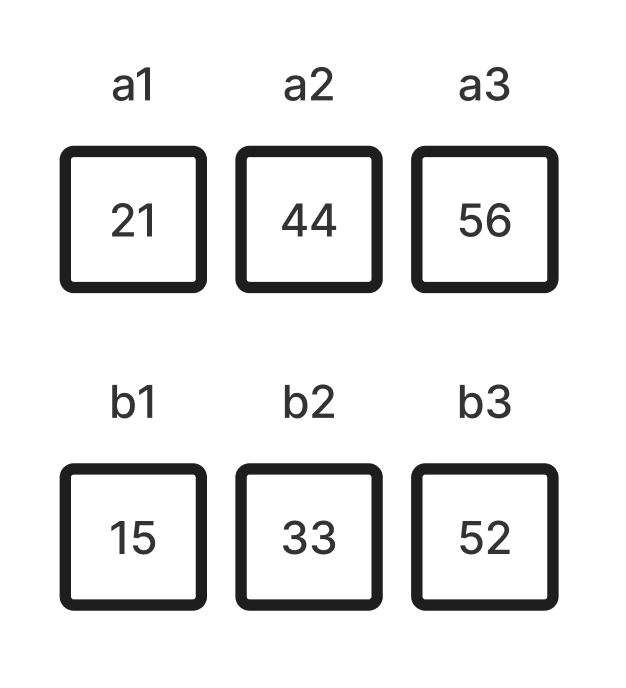
• 배열 두 개를 유심히 살펴보면 a1는 b1보다 크고, a2는 b2보다 크고, a3은 b3보다 크다. 위의 절차를 충실히 따랐으면 a 배열의 k번째 수는, b 배열의 k번째 수보다 항상 클 수 밖에 없다(그렇게 되도록 {큰 값, 작은 값}으로 정렬했으니까). 맨 먼저 b1을 a(큰 값) 배열로 옮기게 될 텐데, b1이 a1보다 항상 작다는 점을 생각하면 다음과 같이 후보군을 찍을 수 있다.

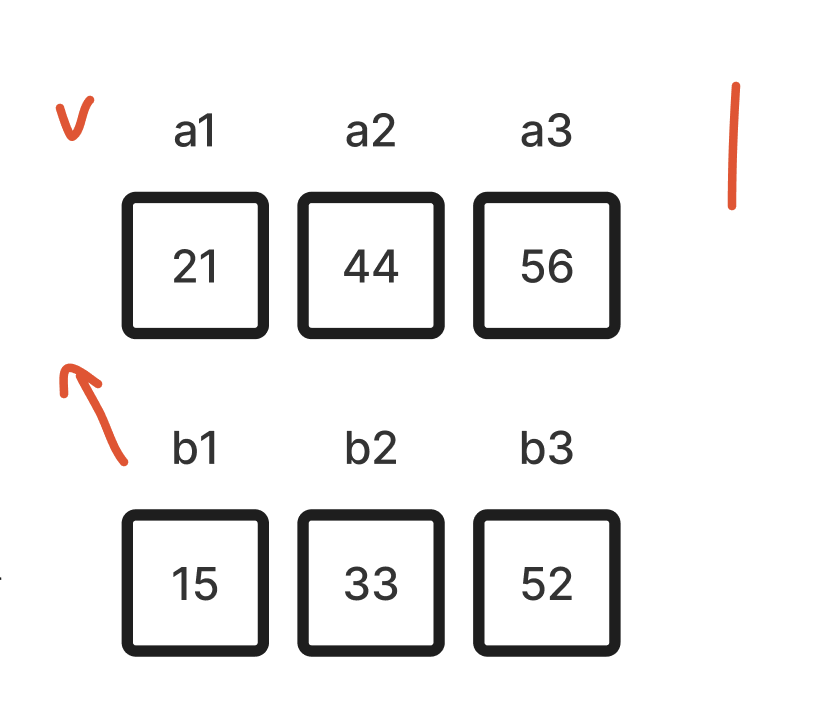
• 경우의 수는 하나로, 최대 1번의 탐색으로 b1(15)을 정렬할 수가 있다. 이진 탐색은 탐색 범위를 절반으로 나누면서 실행하는데, 이미 탐색 범위가 1이기 때문에 이진 탐색 1번으로 적절한 위치를 찾을 수 있다. Jacobstahl 순서를 따른다면, 다음으로 정렬할 수는 52다. b3이 a3보다 항상 작다는 것을 고려했을 때 52의 경우의 수는 아래와 같다.

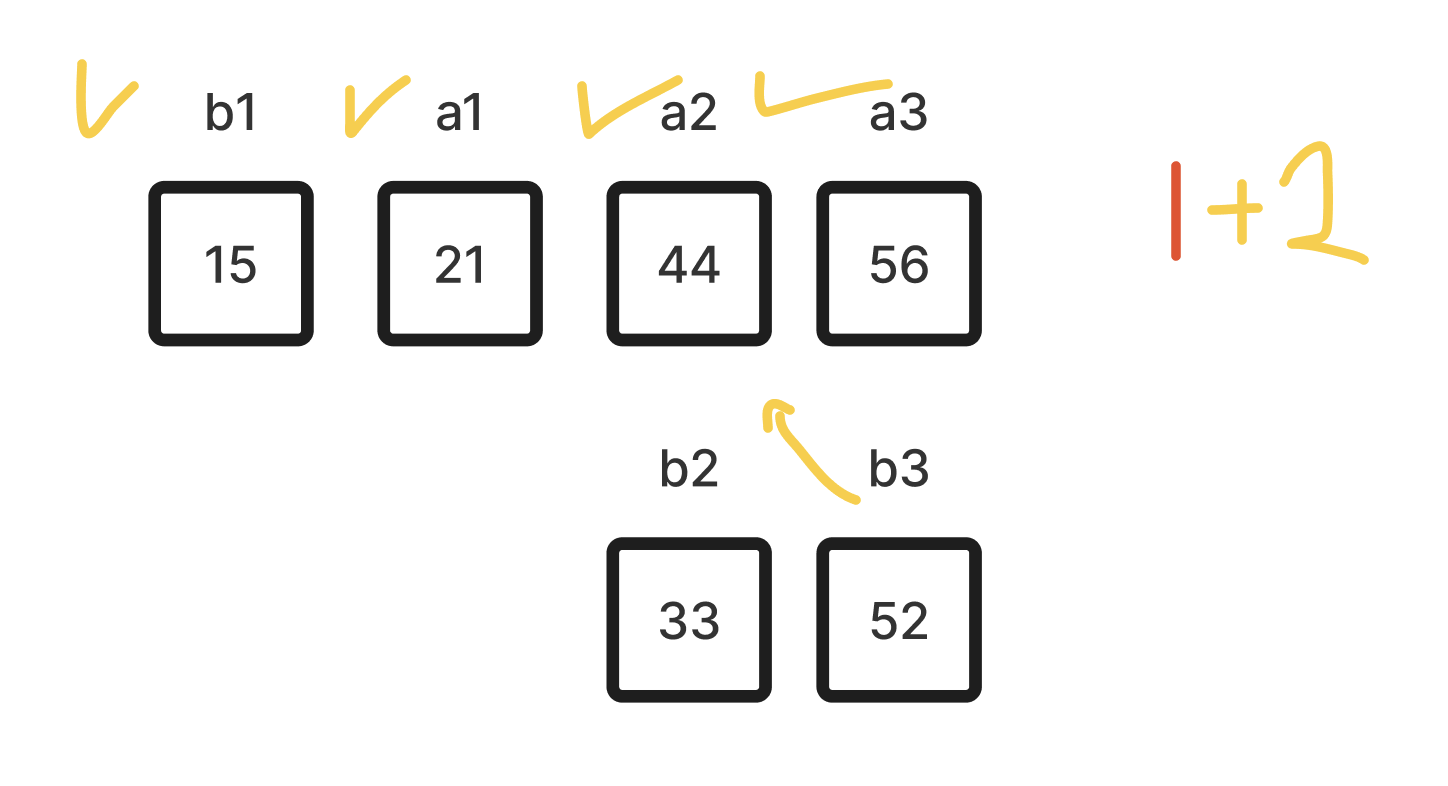
• 52가 위치할 수 있는 4가지의 경우의 수다. 이진 탐색을 최대 2번 실행하는 것으로 52의 위치를 찾을 수 있다. 마지막으로 33을 정렬한다.

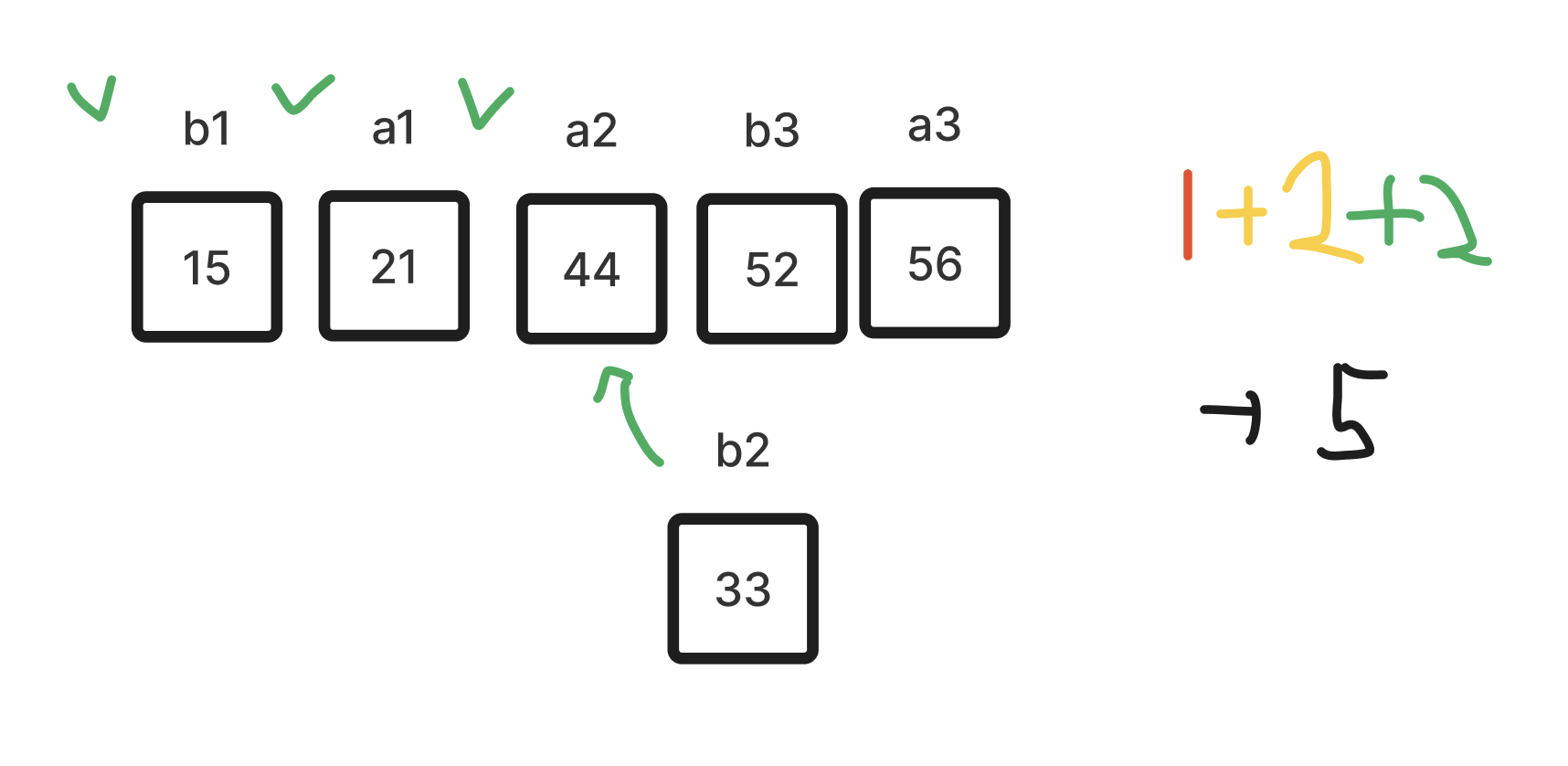
• b2는 a2보다 작기 때문에, 3개의 경우의 수를 가진다. 이 경우 최대 이진 탐색을 2번 실행하여 33의 위치를 찾을 수 있다. 따라서 Jacobstahl 순서를 따를 경우, 5번의 이진 탐색으로 배열을 정렬할 수 있다.

(5 - 2) Jacobstahl 순서를 따르지 않는 경우

• b1을 a에 넣는것 까지는 똑같다. 그 다음으로 33을 정렬한다. 경우의 수는 아래와 같다.

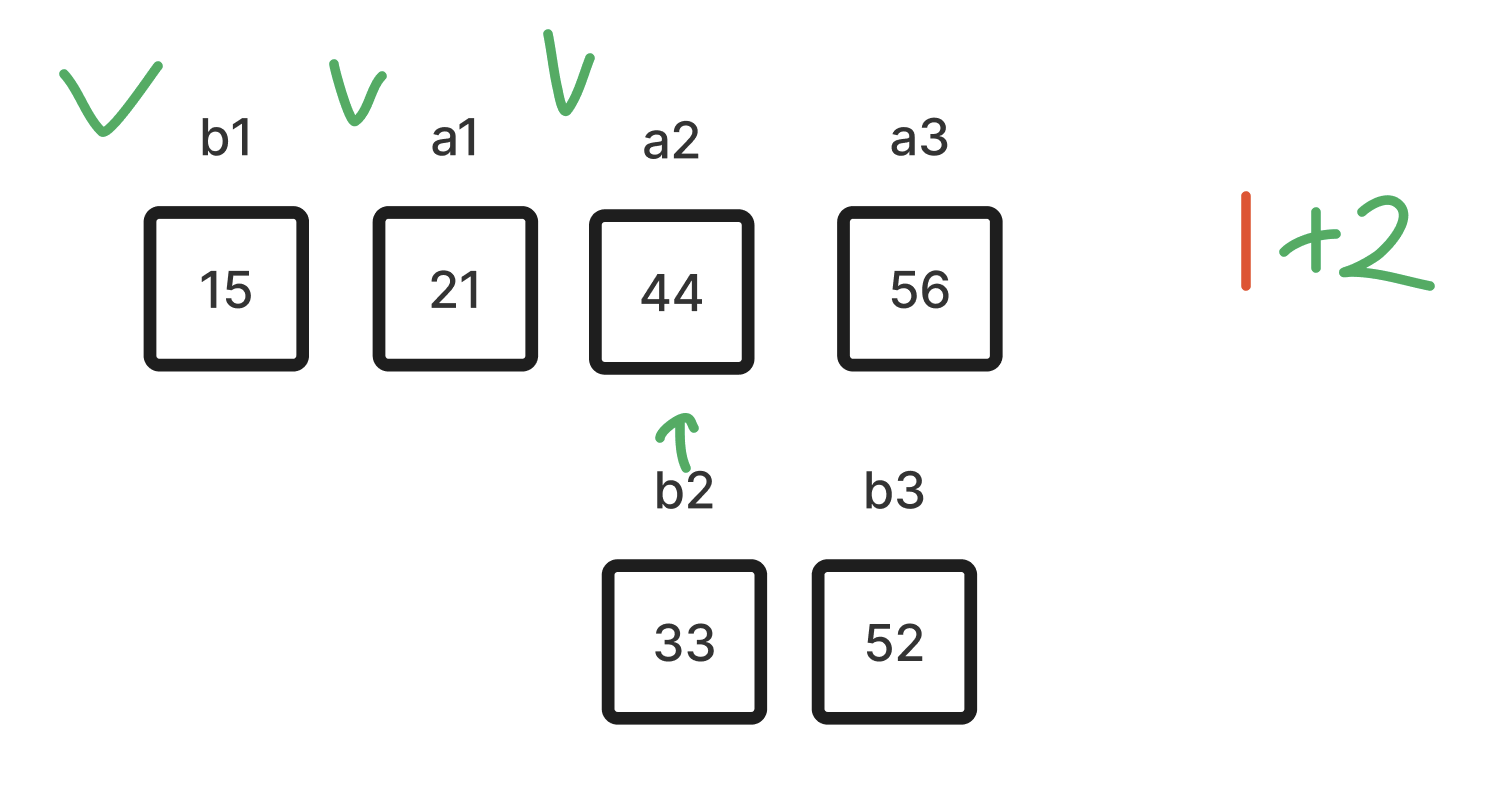
• 경우의 수가 3이므로, 마찬가지로 최대 이진 탐색 2번으로 찾을 수 있다. 마지막으로 44를 정렬한다.

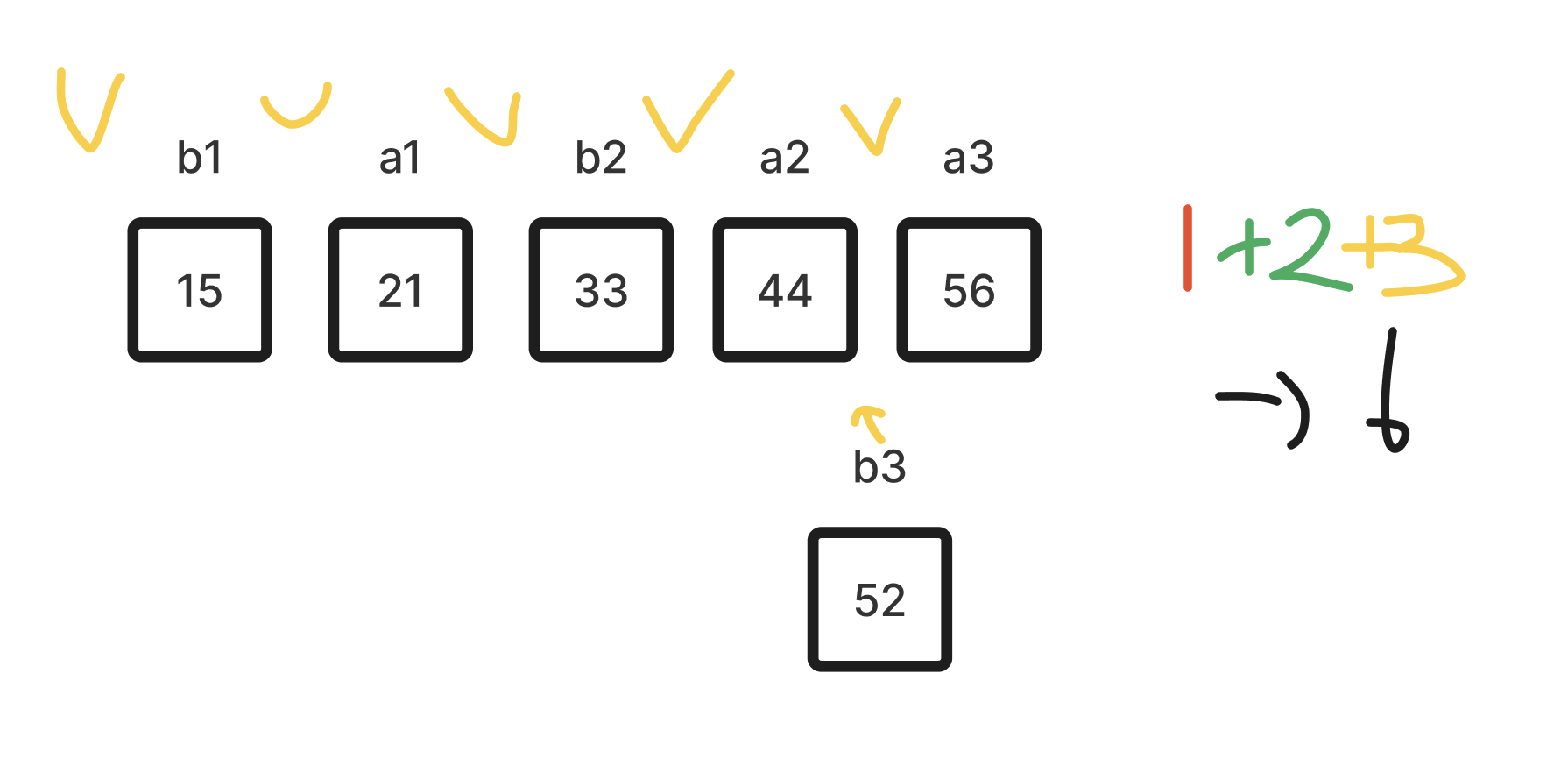
• 탐색 범위가 5이므로, 최대 이진 탐색 3번으로 찾을 수 있다. Jacobstahl 순서를 따르지 않는 경우, 6번의 이진 탐색의 배열을 정렬할 수 있다. Jacobstahl을 따랐을 때보다 이진 탐색 실행 수가 하나 늘어났다. 이런 느낌으로 이진 탐색 수를 줄인다고 보면 되겠다.

• 물론 무조건 이진 탐색 수가 주는 것도 아니다. 만약 a2가 44가 아니라 56보다 더 큰 수였다면? 마지막 52를 정렬하는 경우의 수가 5에서 4로 줄어들면서 최대 이진 탐색 수가 3에서 2로 줄어들고, Jacobstahl 순서로 하나 그냥 하나 같은 이진 탐색 수로 정렬을 하게 되었을 것이다. 운빨똥망정렬

vector와 deque의 std::swap 차이점

std::vector, 그냥 우리가 아는대로 vec[i], vec[i + 1]이 바뀜

std::swap(vec[i], vec[i + 1]);

std::deque, deque a와 deque b간의 swap이 일어남

• 코드 출처 cpp reference, std::swap(std::deque)

#include <algorithm>
#include <iostream>
#include <deque>

int main()
{
    std::deque<int> alice{1, 2, 3};
    std::deque<int> bob{7, 8, 9, 10};

    auto print = [](const int& n) {std::cout << ' ' << n; };

    // Print state before swap
    std::cout << "alice:";
    std::for_each(alice.begin(), alice.end(), print);
    std::cout << "\n" "bob  :";
    std::for_each(bob.begin(), bob.end(), print);
    std::cout << '\n';

    std::cout << "-- SWAP\n";
    std::swap(alice, bob);

    // Print state after swap
    std::cout << "alice:";
    std::for_each(alice.begin(), alice.end(), print);
    std::cout << "\n" "bob  :";
    std::for_each(bob.begin(), bob.end(), print);
    std::cout << '\n';
}

Output:
	alice: 1 2 3
	bob  : 7 8 9 10
	-- SWAP
	alice: 7 8 9 10
	bob  : 1 2 3

std::vector, std::deque, std::list 비교

• 오버헤드(Overhead)란?

 → 어떤 처리를 하기 위해 들어가는 간접적인 처리 시간 · 메모리 등을 말한다

(1) std::vector

* 장점

1) 연속적인 메모리 공간에 저장(물리적으로 연속적)

2) iterator, index로 접근 가능

3) 동적으로 확장 가능한 Dynamic Array로 구현

4) 물리적으로 연속되어 있기 때문에 개별 원소에 대한 접근 속도가 빠름, 끝에서 삽입/제거하는 속도가 가장 빠름.

* 단점

1) 동적으로 확장할 때, 재할당 비용이 꽤 큼

2) Capacity를 확장시켜줄수 있는 적절한 크기의 reserve가 중요(메모리 확보)

💡 vector는 메모리 상의 시퀀스를 유지하기 때문에, 확장을 하게 된다면 새로운 메모리를 할당받아야한다. 따라서 vector는 더 큰 공간을 새로 할당하면서 큰 오버헤드가 발생한다. 이 문제를 reserve라는 함수로 미리 할당하면서 재할당 방지를 하는 것.

(2) std::deque

* 특징

1) random access iterator를 통한 index 접근 가능

2) Dynamic Array로 구현

3) vector와 비슷한 점이 많지만 컨테이너 끝 뿐만 아니라 첫 부분의 삽입/제거도 효율이 높다.

4) 그리고 가장 큰 차이점은 연속된 메모리에 올라가 있지 않다. 몇 바이트 단위의 chunk로 쪼개져 있으며 이 chunk는 내부적으로 관리된다.

* 주의

• 연속적인 메모리 공간이 아니기 때문에, 원소들간 포인터 연산이 불가능하다

(3) std::list

* 특징

1) Double Linked list, 이중 연결 리스트 기반 구현

2) 어느 위치에서도 삽입/제거가 빠르다

* 단점 & 주의

1) index로 접근 불가(처음 또는 끝에서 선형 탐색해야함)

2) 컨테이너 내 원소 순회는 forward/reverse 순회만 가능하며 느림

3) 상호 연결 정보를 위해 추가 메모리 사용

결론

• Jacobstahl수로 이진 탐색 수를 줄이네마네 했지만 이진 탐색 횟수를 줄이는데 큰 역할을 했던 것은 Jacobstahl 순서로 정렬하는게 아니라 a1이 b1보다 크다는 사실(ak가 bk보다 크다는 사실)이었다. 저게 경우의 수를 기가 막히게 줄여서 이진 탐색 수를 엄청 줄여준다. 여러모로 아리송한 exercise였고, 평가자들도 포드-존슨 알고리즘을 정확히 알지 못해 어물쩍 넘어가버렸던 기억이 있다. 다시통과할자신은없다 그래도 푸는 재미가 있는 문제들이었다고 생각한다. 아래는 Jacobstahl 순서로 이진 탐색 + ak가 bk보다 크다는 사실이 적용된 이진 탐색 숫자와, 그것이 적용되지 않은 이진 탐색 숫자를 비교한 출력을 보여주면서 모듈을 끝내도록 하겠다. (정수 2000개를 정렬하였다)

(1) “Jacobstahl 순서로 이진 탐색 + ak가 bk보다 크다” 적용됨 -> 이진 탐색 수 9488회

(2) 적용 안됨 -> 이진 탐색 수 10361회

• 결국 어찌됐든 이진 탐색 수를 줄였다는 것을 보여줘야 하는 exercise가 아닌가 하는 생각이다. 이것으로 cpp module을 마친다.