연결 리스트(BOJ 5397 키로거, BOJ 1158 요세푸스 문제)
“0x04강 - 연결리스트 (2)”
복습
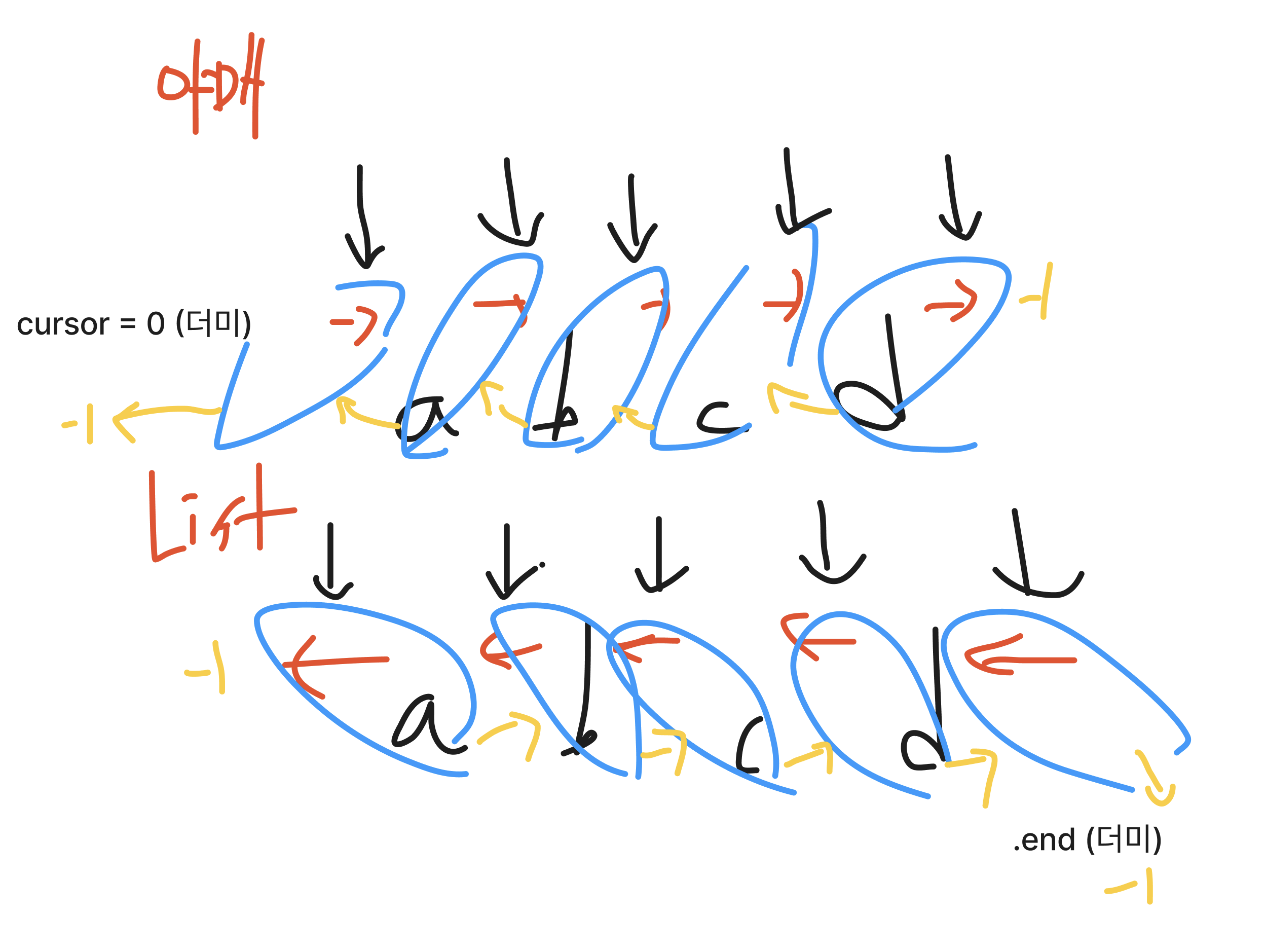
- 연결 리스트 관련 문제를 풀 때, 놀랍게도 도움이 아주 많이 되었다.
| 메서드 | insert | erase |
|---|---|---|
| 야매 리스트 | 현재 iter 오른쪽에 insert함 (반환값 없음) | 왼쪽을 erase함 (반환값 없음) |
| STL list | 현재 iter 왼쪽에 insert함 (insert한 노드의 iterator를 반환하지만 여기선 굳이 반환값을 사용하지 않음) | 오른쪽을 erase함 (erase한 다음 노드를 반환함) |
BOJ 5397 키로거
#include <iostream>
#include <algorithm>
#include <vector>
#include <string>
#include <stack>
#include <queue>
#include <deque>
#include <map>
#include <list>
#include <utility>
#define all(x) (x).begin(), (x).end()
#define rep(i, a, b) for (int i = (a); i < (b); ++i)
using namespace std;
int tc;
void solve(string s)
{
list<char> l;
list<char>::iterator it = l.begin();
for (int i = 0; i < s.length(); i++) {
if (s[i] == '<') {
if (it != l.begin())
it--;
}
else if (s[i] == '>') {
if (it != l.end())
it++;
}
else if (s[i] == '-') {
if (it != l.begin()) { // 예외처리 필요함
it--;
it = l.erase(it);
}
}
else {
l.insert(it, s[i]);
}
}
for (list<char>::iterator it = l.begin(); it != l.end(); it++)
{
cout << *it;
}
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL);
cin >> tc;
while (tc--) {
string s;
cin >> s;
solve(s);
cout << endl;
}
return 0;
}
- 백스페이스(‘-‘)일때, iterator를 한칸 물리는 과정에서, begin일 때의 예외처리를 안 했더니, begin일 때도 iterator를 물려버려서 double free오류가 발생함. 예외 처리를 잘하자
BOJ 1158 요세푸스 문제
#include <iostream>
#include <algorithm>
#include <vector>
#include <string>
#include <stack>
#include <queue>
#include <deque>
#include <map>
#include <list>
#include <utility>
#define all(x) (x).begin(), (x).end()
#define rep(i, a, b) for (int i = (a); i < (b); ++i)
using namespace std;
//|1|4|5|
int N, K;
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL);
cin >> N;
cin >> K;
list<int> l;
vector<int> v;
for (int i = 1; i <= N; i++)
l.push_back(i);
list<int>::iterator it = l.begin();
for (int i = 0; i < N; i++)
{
for (int i = 0; i < K - 1; i++)
{ // 노드의 오른쪽을 가리키는 list 특징상, K - 1번씩 반복문을 돌려야함
it++;
if (it == l.end())
it = l.begin();
}
v.push_back(*it);
it = l.erase(it);
// erase했을 때, iterator의 반환값이 딱 end일때,
// begin으로 돌려놓는 과정이 필요함. 안그럼 값이 하나씩 밀림
if (it == l.end())
it = l.begin();
}
cout << "<";
for (int i = 0; i < v.size(); i++) {
cout << v[i];
if (i != v.size() - 1)
cout << ", ";
}
cout << ">";
return 0;
}
- 이 문제의 경우, 원형 연결 리스트를 쓰면 편했을까 하는 생각이 들었다. end와 begin이 이어져 있지 않은 list의 경우, iterator가 end를 가리킬때, 그것을 begin으로 돌려놓는 것이 중요하다. end는 더미 노드이므로 iterator가 end를 가리키는 것은 허수다.
메모
(1) 손코딩 문제 1
문제 - 원형 원결 리스트 내의 임의의 노드 하나가 주어졌을 때 List의 길이를 효율적으로 구하기
정답 - 동일한 노드가 나올 때까지 계속 다음 노드로 가면 됨, 공간복잡도 O(1), 시간복잡도 O(N)
(2) 손코딩 문제 2
문제 - 중간에 만나는 두 연결 리스트의 시작점이 주어졌을 때 만나는 지점을 구하는 방법
정답 - 두 시작점 각각에 대해 끝까지 진행시켜 각 리스트의 길이를 구한다. 이후 다시 시작점으로 돌아와 더 긴쪽을 둘의 차이만큼 앞으로 이동시켜놓고, 두 시작점이 만날 때까지 두 시작점을 동시에 한칸씩 전진시킨다. 공간복잡도 O(1), 시간복잡도 O(A+B)
(3) 손코딩 문제 3
- 문제 -
주어진 연결 리스트에 사이클이 있는지 판단한다.
정답 - Floyd’s cycle-finding Algorithm, 공간복잡도 O(1), 시간복잡도 O(N)
- Floyd’s cycle-finding Algorithm : 한 칸씩 가는 커서와 두 칸씩 가는 커서를 동일한 시작점에서 출발시키면 사이클이 있을 경우 두 커서는 반드시 만나게 된다. 반대로 만약 사이클이 없으면 두 커서가 만나지 못하고 연결 리스트의 끝에 도달한다. 이 알고리즘을 이용하면 거치는 모든 노드를 저장할 필요가 없이 공간복잡도 O(1)에 사이클의 존재 여부를 알 수 있다.
