BOJ 1043 - 거짓말
“유니온 파인드”
BOJ 1043 - 거짓말
문제 링크

#include <bits/stdc++.h>
typedef long long ll;
const int INF = 0x3f3f3f3f;
using namespace std;
int n, m, k;
int p[52];
vector<int> know;
vector<int> party[52]; // 변경된 부분
int Find(int x) {
if (p[x] == x)
return x;
return x = Find(p[x]);
}
void Union(int x, int y) {
int px = Find(x);
int py = Find(y);
p[px] = py;
}
int main(void) {
ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
cin >> n >> m >> k;
while (k--) {
int t;
cin >> t;
know.push_back(t);
}
for (int i = 1; i <= n; i++)
p[i] = i;
int p, num, prev;
for (int i = 0; i < m; i++)
{
int p; cin >> p;
for (int j = 0; j < p; j++) {
if (j >= 1) {
prev = num; cin >> num;
Union(prev, num);
}
else
cin >> num;
party[i].push_back(num);
}
}
int res = m;
for (int i = 0; i < m; i++) {
bool flag = false;
for (int j = 0; j < party[i].size(); j++)
{
if (flag)
break;
for (int k = 0; k < know.size(); k++)
{
if (Find(party[i][j]) == Find(know[k]))
{
flag = true;
break;
}
}
}
if (flag)
res--;
}
cout << res;
return 0;
}
이 문제는 유니온 파인드를 사용하는 서로소 집합 표현 문제이다. 즉 주어진 그래프 내에서 진실을 아는 사람(정점)과 그렇지 않은 사람들을 구분하여, 총 파티 수에서 진실을 모르는 사람들만 참가한 파티의 수를 제하면 된다.
Input이 아래와 같을 때, 참가할 수 있는 총 파티의 개수는 0.
3 4 // 총 3명의 사람, 총 4개의 파티
1 3 // 진실을 아는 사람 1명 (3번 사람)
1 1 // 첫 번째 파티 참가자 1명 (1번 사람)
1 2 // 두 번째 파티 참가자 1명 (2번 사람)
2 1 2 // 세 번째 파티 참가자 2명 (1, 2번 사람)
3 1 2 3 // 네 번째 파티 참가자 3명 (1, 2, 3번 사람)
output: 0
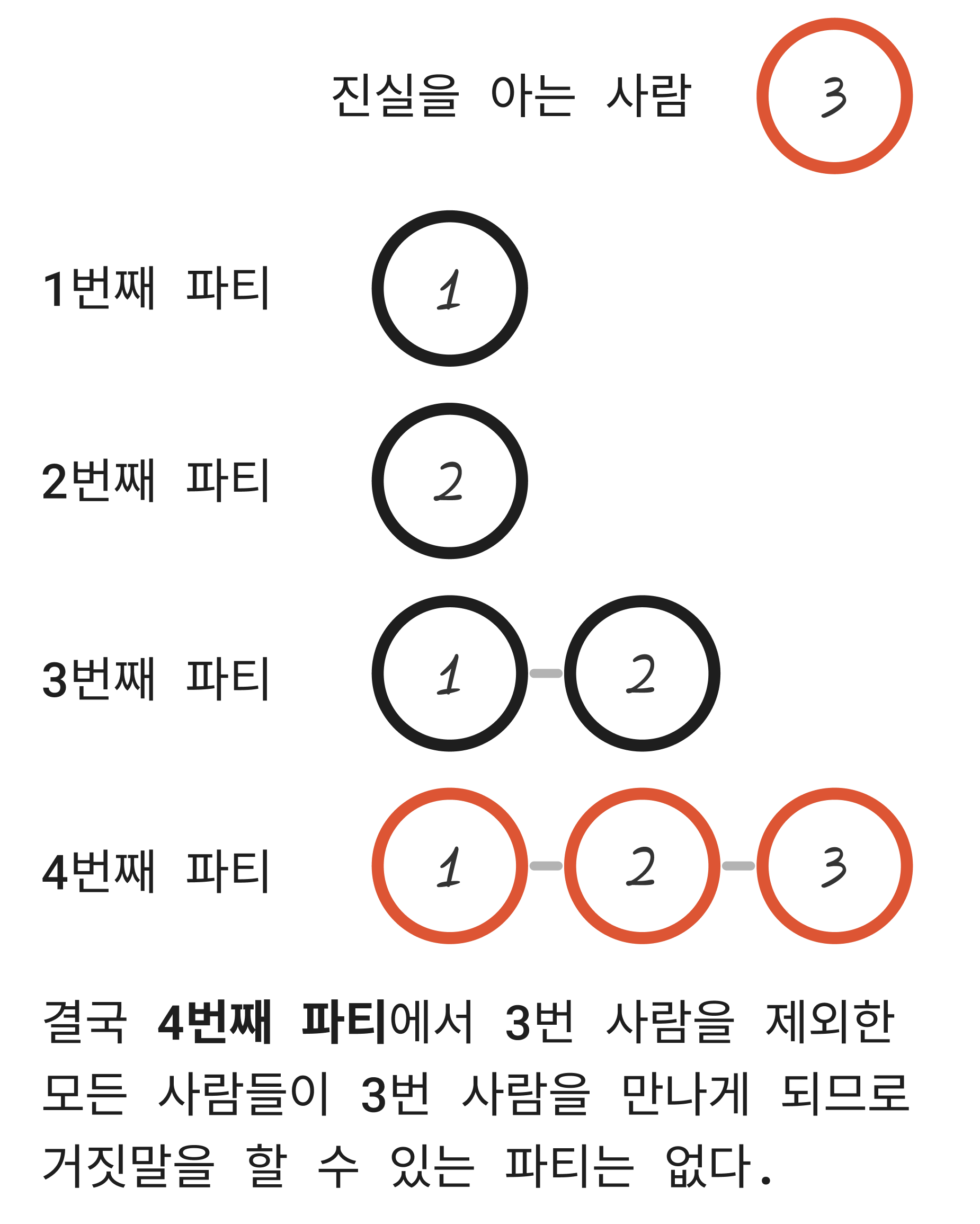
이런 식으로 진실을 모르는 사람이라 할지라도 진실을 아는 사람이 참가한 파티에 같이 참가한 경우 지민이가 거기서 진실을 말했을 것이기 때문에 어쨋든 진실을 알게 되고, 진실을 모른다 해도 지민이는 그런 사람들 앞에서 거짓말을 할 수가 없게 되어버린다(거짓말이 들통이 나기 때문).
파티에 참가하는 총 사람 수가 많이 주어지고, 진실을 아는 사람과 모르는 사람이 마구 뒤섞여서 파티에 참가하는 입력의 경우, 진실을 모르는 사람이면서 동시에 진실을 아는 사람들이 참가하는 파티에 참가하지 않는 사람을 가려내는 것이 매우 어렵다. 이때 유니온 파인드를 사용하면 쉽게 사람들을 걸러낼 수 있다. 골자는 진실을 모르는 사람과 진실을 아는 사람이 파티에 섞여 참가했을 떄, 두 사람을 한 그룹으로 묶어놓는 것이다. 그러면 진실을 아는 사람의 그룹과 그렇지 못한 그룹으로 나뉘게 되고, 그 그룹을 가지고 다시 파티를 체크해서 진실을 모르는 사람만이 참가한 파티의 수를 구하면 된다.
유니온 파인드는 크게 두 가지 절차로 이루어진다. 하나는 두 노드의 그룹을 하나로 묶는 Union(한 노드의 부모를 다른 노드로 변경하여 하나의 그룹으로 묶는다)이고, 다른 하나는 특정 노드의 부모를 찾는 Find다. 물론 처음 시작할 때 각 노드의 부모는 자기 자신이다. 그 상태에서 진실을 아는 사람과 모르는 사람이 함께 파티에 참가했을 때, 앞 사람의 부모 노드가 뒷 사람의 부모 노드를 가리키게 함으로써 두 사람을 한 그룹으로 묶는다. 그러면 파티를 전부 순회했을 때, 진실을 말해야 하는 사람과 거짓말을 해도 되는 사람의 그룹으로 깔끔하게 나뉘게 되고, 다시 파티를 순회하면서 거짓말을 해도 되는 사람만이 참가한 파티를 찾을 수가 있게 된다.
Union의 코드는 아래와 같다. 배열 p의 인덱스 x(
p[x])의 값이 노드 x의 부모이다.
void Union(int x, int y) {
int px = Find(x); // Find 함수는 x 노드의 부모를 찾는다.
int py = Find(y); // y 노드의 부모를 찾는다.
p[px] = py; // px의 부모를 py로 한다. 이러면 x와 y는 같은 그룹에 속하게 된다.
}
두 노드 x와 y가 주어졌을 때, Find 함수로 각각의 두 노드의 부모를 찾고, x 노드의 부모의 부모 노드를 y 부모의 부모 노드로 한다. 이렇게 하면 x 노드와 y 노드가 같은 그룹에 속하게 된다.
Find 함수는 아래와 같다.
int Find(int x) {
if (p[x] == x) return x;
return x = Find(p[x]);
}
만약 노드 x의 부모가 자기 자신이 아니라면 그 노드는 무조건 어떤 다른 노드의 자식이라는 의미이기 때문에,
Find(x)의 반환값이 자기 자신일때까지 재귀를 돌려서 부모 노드를 찾아낸다.이제 파티를 다시 순회하면서 진실을 아는 그룹이 속한 파티의 수만큼, 총 파티 개수에서 차감한다.
for (int i = 0; i < m; i++) {
bool flag = false;
for (int j = 0; j < party[i].size(); j++)
{
if (flag)
break;
for (int k = 0; k < know.size(); k++)
{
if (Find(party[i][j]) == Find(know[k]))
{ // 여기가 핵심!
flag = true;
break;
}
}
}
if (flag)
res--;
}
cout << res;
- 사실 글로만 설명하면 잘 안와닿는데, 직접 그려서 해보면 잘 되는 것을 알아보기 쉽다. 잘 숙지해서 유니온 파인드 문제들을 풀어보자.
