백트래킹
“0x0C강 - 백트래킹”
백트래킹
워크북
| 분류 | 백준 번호 | 문제 제목 |
|---|---|---|
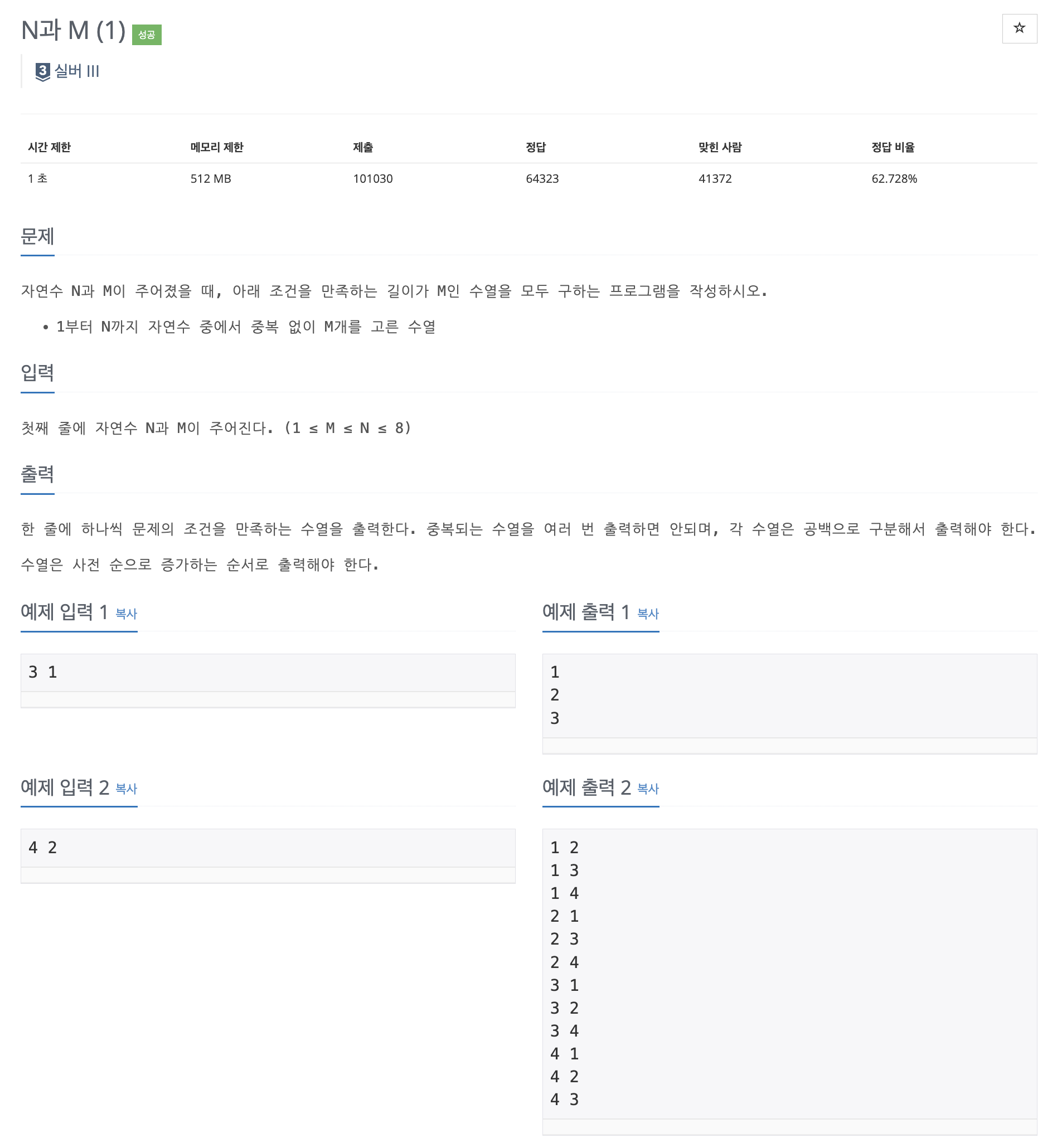
| 연습 문제 | 15649 | N과 M (1) |
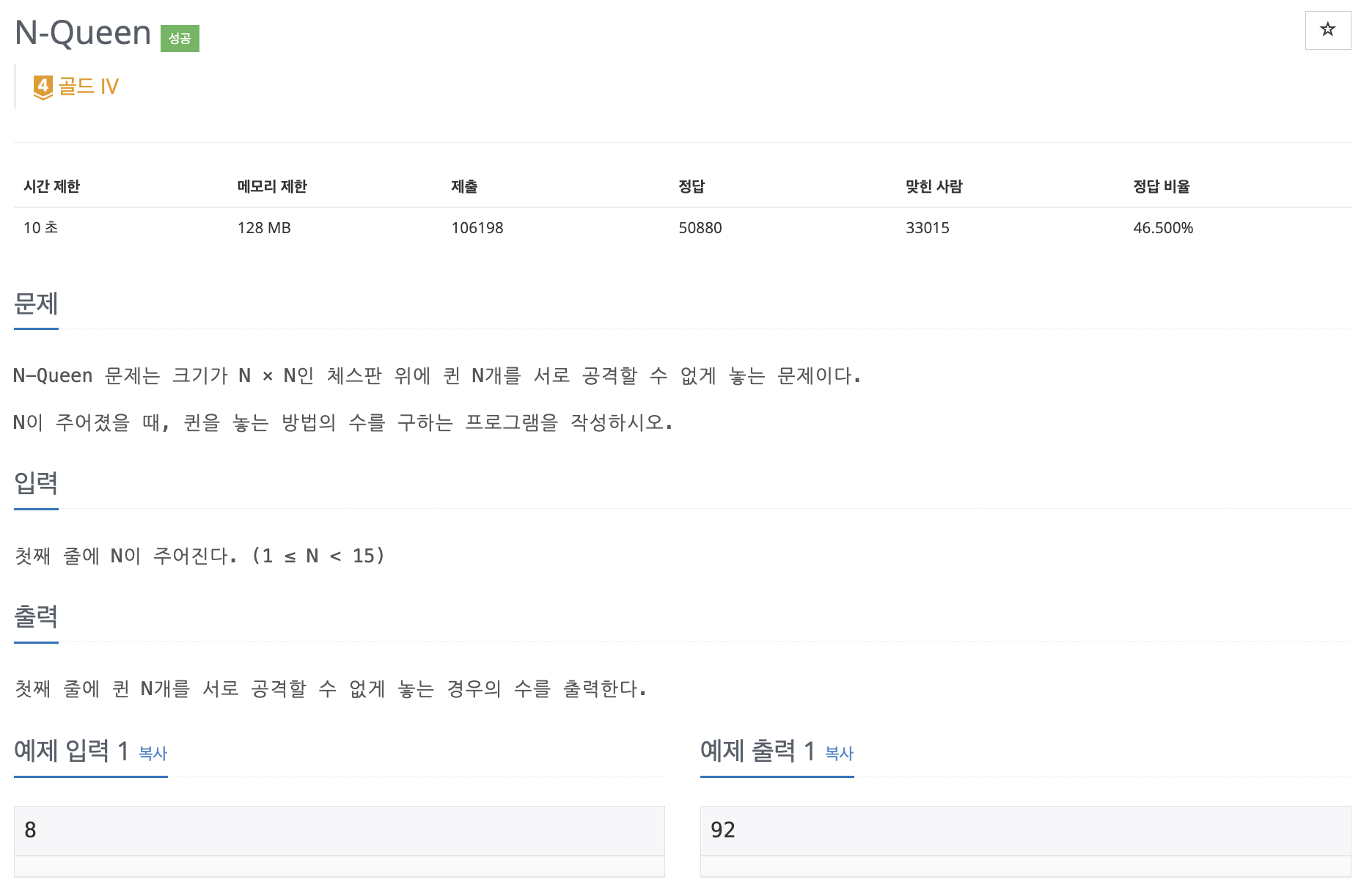
| 연습 문제 | 9663 | N-Queen |
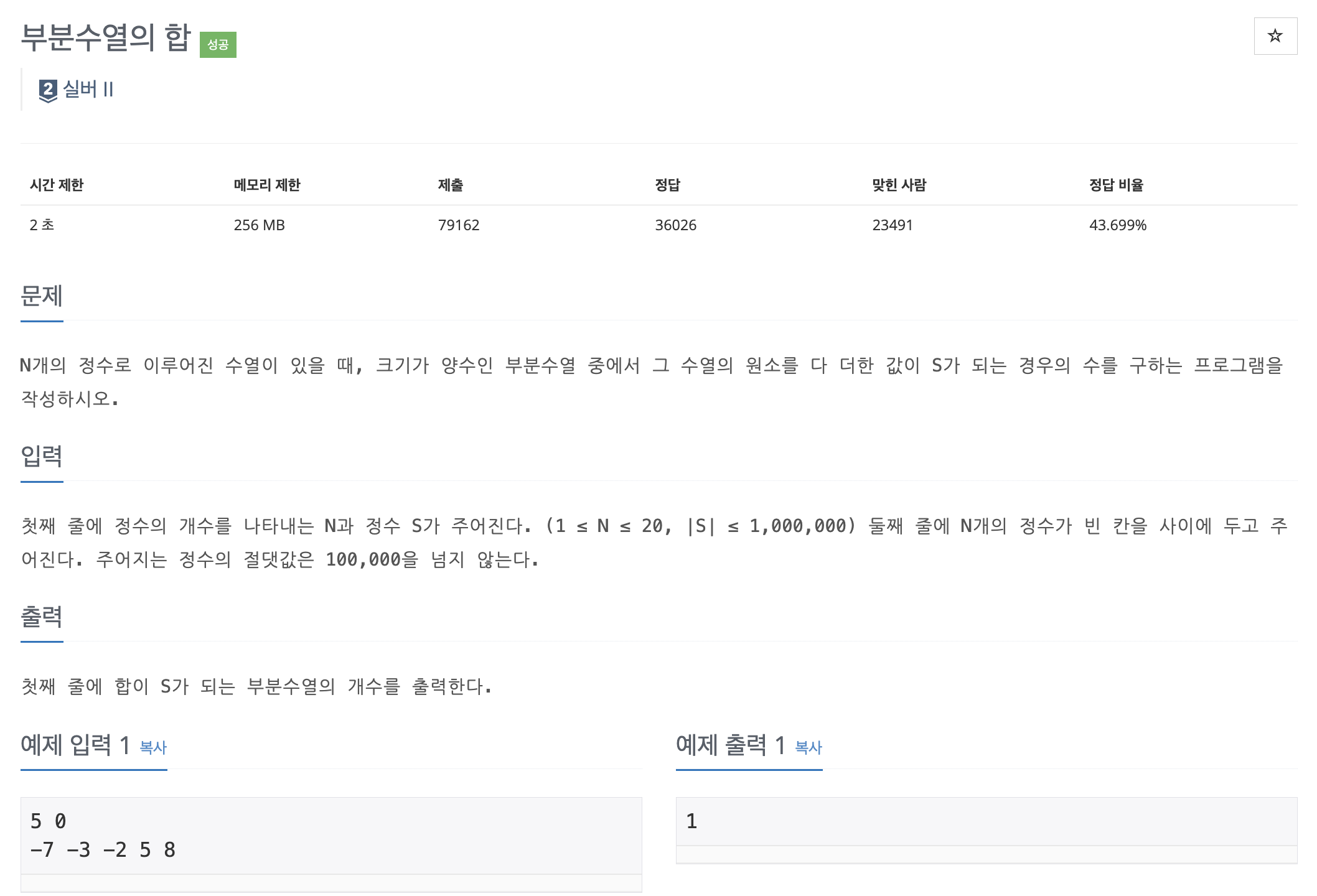
| 연습 문제 | 1182 | 부분수열의 합 |
| 기본 문제✔ | 15650 | N과 M (2) |
| 기본 문제✔ | 15651 | N과 M (3) |
| 기본 문제✔ | 15652 | N과 M (4) |
| 기본 문제✔ | 15654 | N과 M (5) |
| 기본 문제✔ | 15655 | N과 M (6) |
| 기본 문제✔ | 15656 | N과 M (7) |
| 기본 문제✔ | 15657 | N과 M (8) |
| 기본 문제✔ | 15663 | N과 M (9) |
| 기본 문제✔ | 15664 | N과 M (10) |
| 기본 문제✔ | 15665 | N과 M (11) |
| 기본 문제✔ | 15666 | N과 M (12) |
| 기본 문제✔ | 6603 | 로또 |
BOJ 15649, N과 M (1)
#include <bits/stdc++.h>
using namespace std;
int N, M; // 4 3
int arr[10];
int isused[10];
void func(int k)
{
if (k == M) {
for (int i = 0; i < M; i++)
cout << arr[i] << ' ';
cout << '\n';
return ;
}
for (int i = 1; i <= N; i++) {
if (!isused[i]) {
arr[k] = i;
isused[i] = 1;
func(k + 1);
isused[i] = 0;
}
}
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL);
cin >> N >> M;
func(0);
return 0;
}
for (int i = 1; i <= N; i++) {
if (!isused[i]) {
arr[k] = i;
isused[i] = 1;
func(k + 1);
isused[i] = 0;
}
}
- 이 반복문이 백트래킹의 전형적인 구조라고 한다. 반복문을 돌면서 arr를 채워넣고, 특정 수를 채워넣었다는 것을 체크하는 isused 배열을 1로 바꾸고 재귀를 타고 들어가는 구조다. 이 반복문은 N과 M 모든 시리즈에 사용되기 때문에, 이 반복문만 이해한다면 모든 N과 M 문제를 풀 수 있게 된다.
BOJ 9663, N-Queen
#include <bits/stdc++.h>
using namespace std;
int col[15];
int N, sum;
bool check(int m)
{
for (int i = 0; i < m; i++) {
if (col[i] == col[m] || abs(col[i] - col[m]) == abs(i - m))
return false;
}
return true;
}
void func(int m)
{
if (m == N) {
sum++;
}
else {
for (int i = 0; i < N; i++)
{
col[m] = i;
if (check(m))
func(m + 1);
}
}
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL);
cin >> N;
func(0);
cout << sum;
return 0;
}
피신에서 비슷한 문제를 풀어본 적이 있다. ~풀어본 적만 있다.~
퀸의 이동 경로 때문에, 한 행에는 반드시 하나의 퀸만 위치할 수 있다. 따라서 우리는 input N을 받은 후 크기가 N인 일차원 배열 col[N]을 선언하여 퀸의 위치를 저장할 수 있다.
이후 0번째 열부터 시작하면서, 0번째 행부터 차례로 퀸을 놓기 시작하여 조건에 맞으면 계속해서 퀸을 놓아나가고, N번째 퀸을 놓는데 성공했다면 경우의 수를 늘린다. 이때 퀸의 위치가 적절한 지 따지는 함수가 중요하다.
bool check(int m)
{
for (int i = 0; i < m; i++) {
if (col[i] == col[m] || abs(col[i] - col[m]) == abs(i - m))
return false;
}
return true;
}
col[i]는 행(x)번호,i는 열 번호를 의미한다. 같은 라인(행)에 있거나, 혹은 대각선에 있는 경우 false를 반환한다.
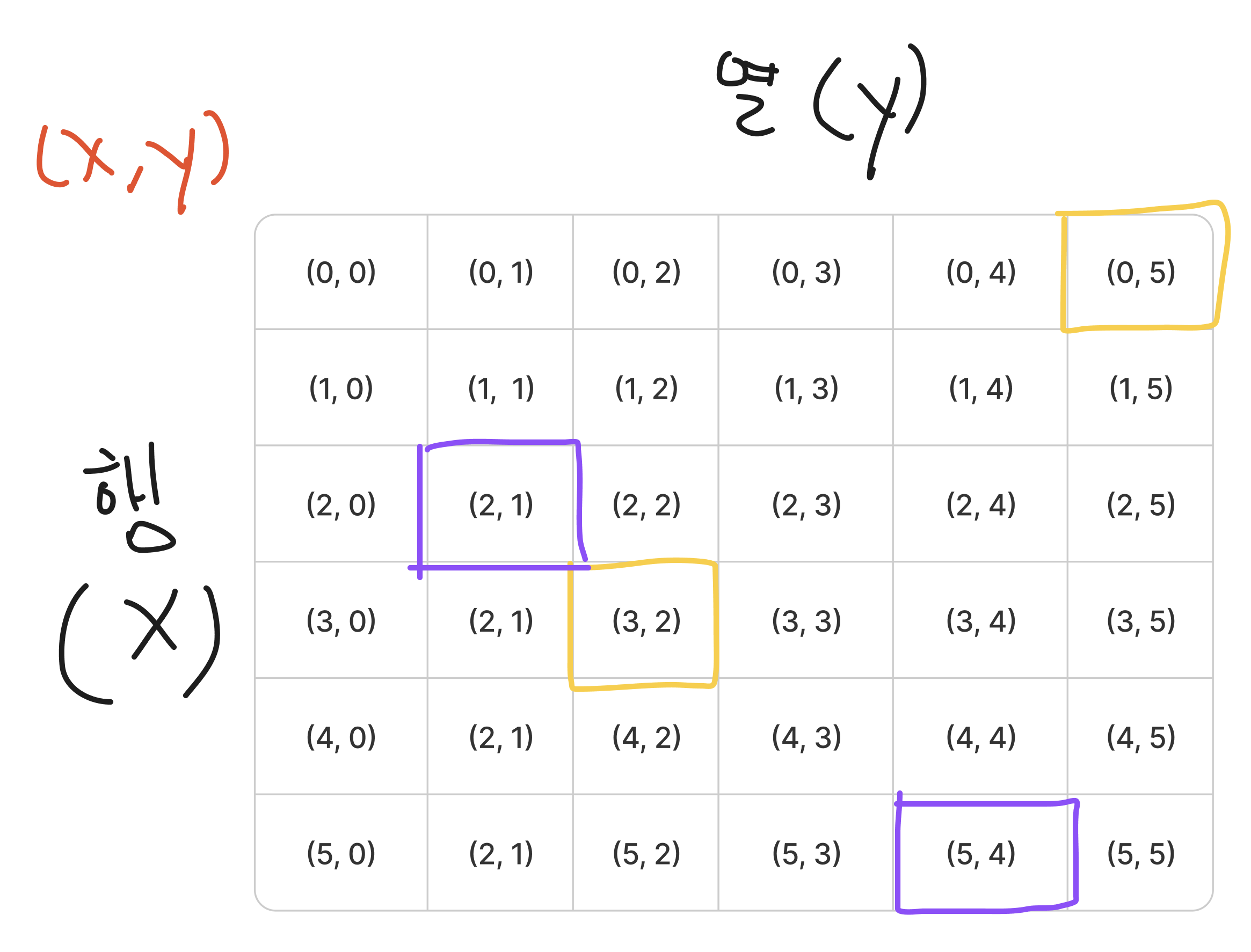
- 보라색으로 표시한 두 좌표와, 노란색으로 표시한 두 좌표가 대각선 관계다.
abs(col[i] - col[m]) == abs(i - m)
- 가 성립하면 대각선 관계다. (2, 1) 과 (5, 4) 그리고 (3, 2) 와 (0, 5)는 위의 수식이 성립한다. 아까 말했듯이
col[i]는 x좌표,i는 y좌표기 때문에
x y x y
(2, 1) (5, 4)
=> abs(5 - 2) = abs(4 - 1)
x y x y
(3, 2) (0, 5)
=> abs(0 - 3) = abs(5 - 2)
- 임을 확인할 수 있다.
BOJ 1182, 부분수열의 합
#include <bits/stdc++.h>
using namespace std;
int N, S;
int arr[30];
int cnt = 0;
void func(int cur, int sum) {
if (cur == N) {
if (sum == S)
cnt++;
return ;
}
func(cur + 1, sum);
func(cur + 1, sum + arr[cur]);
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL);
cin >> N >> S;
for (int i = 0; i < N ; i++)
cin >> arr[i];
func(0, 0);
if (S == 0)
cnt--;
cout << cnt;
return 0;
}
- k번째 재귀에서 k번째 수를 더하거나 더하지 않거나로 두 가지로 재귀를 뻗어나가면 되는, 언뜻 생각하면 어렵지 않은 재귀지만 앞에서 N과 M 백트래킹 반복문에 도취되어 있던 나는 쉽사리 이 재귀를 생각해내지 못했다…
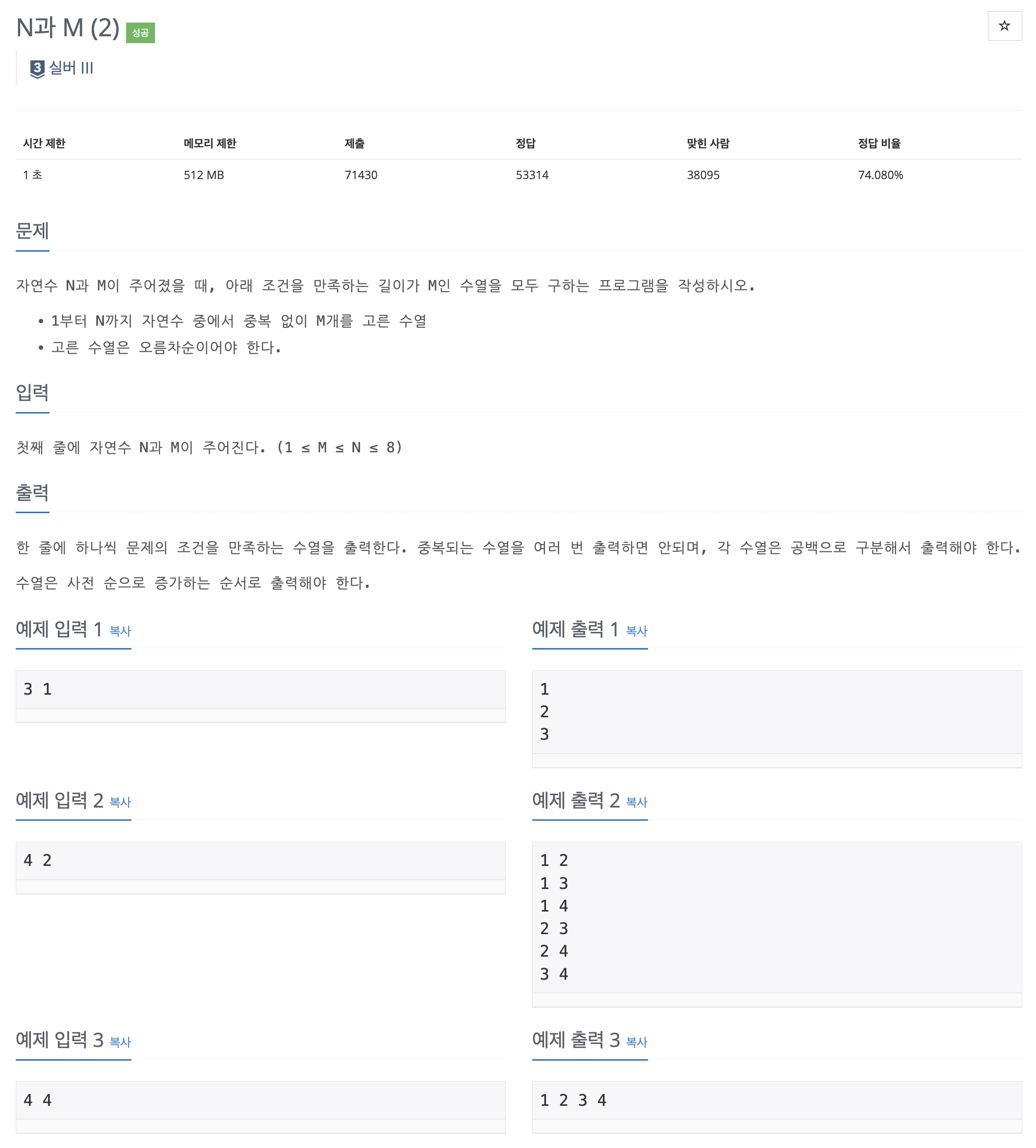
BOJ 15650, N과 M (2)
풀이 1
#include <bits/stdc++.h>
using namespace std;
int N, M;
int arr[8];
int isused[8];
void solve(int k)
{
if (k == M) {
for (int i = 0; i < M; i++) {
cout << arr[i] << ' ';
}
cout << '\n';
return ;
}
for (int i = 1; i <= N; i++) {
arr[k] = i;
if (k > 0 && arr[k - 1] >= arr[k])
continue ;
solve(k + 1);
}
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL);
cin >> N >> M;
solve(0);
return 0;
}
풀이 2
#include <bits/stdc++.h>
using namespace std;
int N, M;
int arr[10];
int isused[10];
void solve(int k)
{
if (k == M) {
for (int i = 0; i < M; i++) {
cout << arr[i] << ' ';
}
cout << '\n';
return ;
}
int st = 1;
if (k != 0)
st = arr[k - 1] + 1;
// arr[0]이 2면 st는 3이됨
for (int i = st; i <= N; i++) {
if (!isused[i]) {
arr[k] = i;
isused[i] = 1;
solve(k + 1);
isused[i] = 0;
}
}
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL);
cin >> N >> M;
solve(0);
return 0;
}
N과 M (1)과 다르게 고른 수열이 오름차순이어야 한다는 조건이 추가되었다. 따라서 k + 1번째 수는 반드시 k번째 수보다 커야만 한다. 따라서 k + 1번째 수가 k번째 수보다 작을 때, 그 수열은 넘어가기 위한 조건이 필요하다. 풀이 1은 내가 생각해낸 조건인데, 직관적이긴 한데 백트래킹이라는 컨셉트에서 좀 벗어난 것 같다.
풀이 2는 바킹독 문제집의 정해 코드인데 따로 st라는 숫자를 두고 st가 arr[k]보다 반드시 크도록 만들어서 애초에 k + 1번째 수가 k번째 수보다 작은 상황을 만들지 않는다. 과연 현명한 풀이…
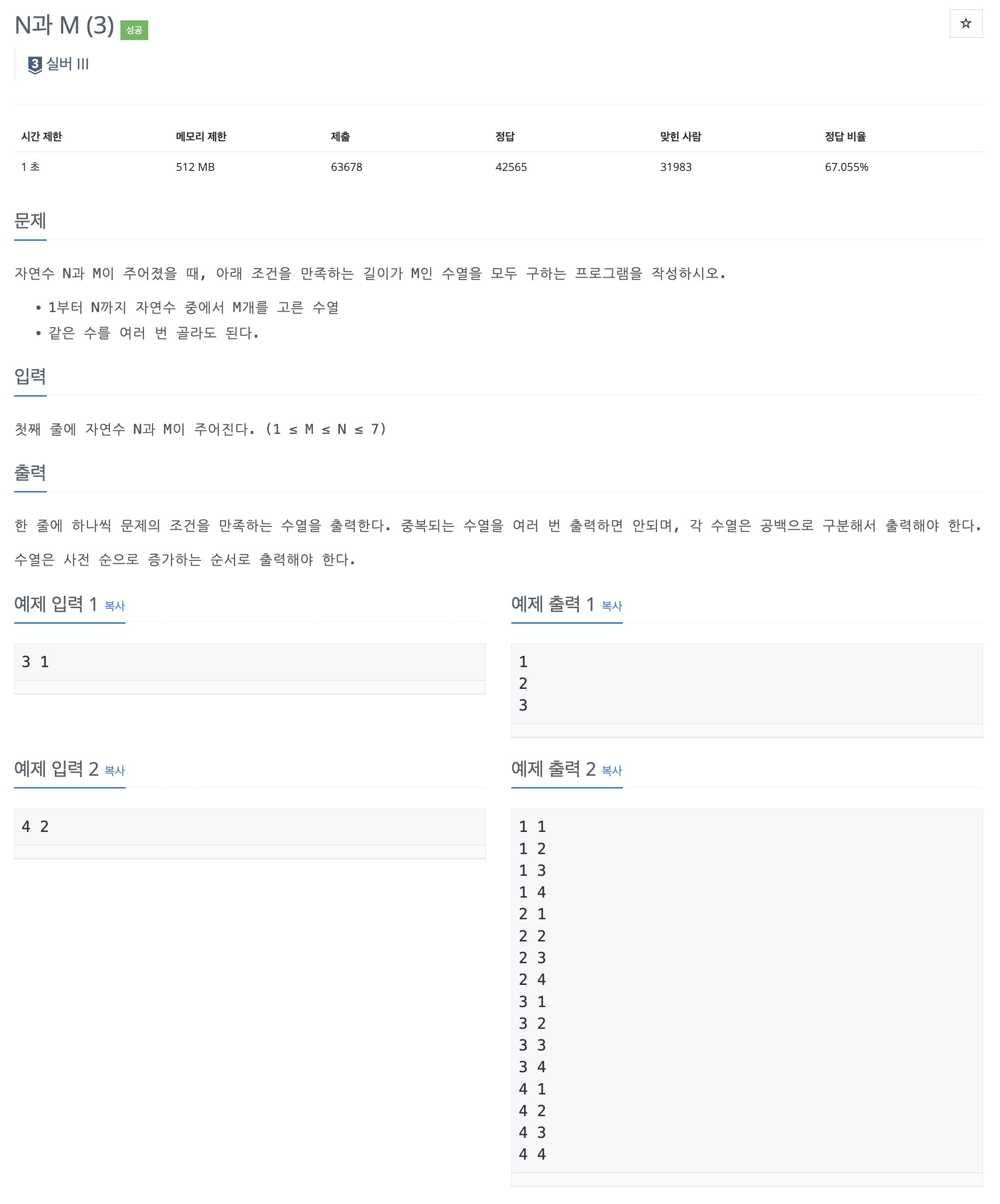
BOJ 15651, N과 M (3)
#include <bits/stdc++.h>
using namespace std;
int N, M;
int arr[10];
int isused[10];
void solve(int k)
{
if (k == M)
{
for (int i = 0; i < M; i++)
cout << arr[i] << " ";
cout << '\n';
return ;
}
for (int i = 1; i <= N; i++) {
arr[k] = i;
solve(k + 1);
}
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL);
cin >> N >> M;
solve(0);
return 0;
}
- N과 M (1)에서 같은 수를 여러 번 골라도 된다는 조건이 추가되었다. isused 배열을 사용했던 이유가 중복을 체크하기 위함이었기 때문에, 중복해서 수를 골라도 된다면 굳이 isused 배열을 사용할 필요가 없이 바로 다음 재귀로 들어가면 된다.
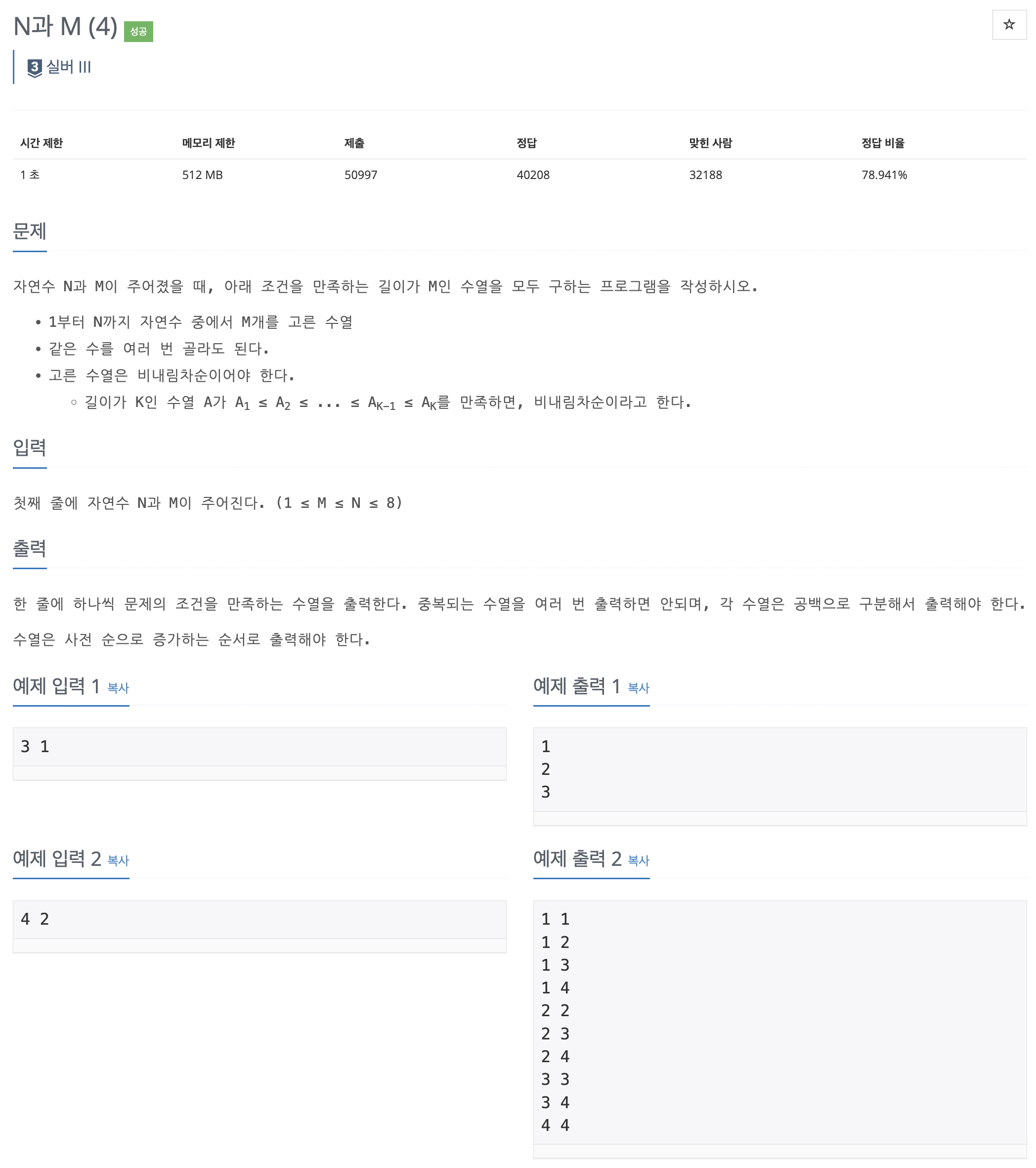
BOJ 15652, N과 M (4)
풀이 1
#include <bits/stdc++.h>
using namespace std;
int N, M;
int arr[10];
int isused[10];
void solve(int k)
{
if (k == M) {
for (int i = 0; i < M; i++)
cout << arr[i] << ' ';
cout << '\n';
return ;
}
for (int i = 1; i <= N; i++)
{
arr[k] = i;
if (k > 0 && arr[k - 1] > arr[k])
continue ;
solve(k + 1);
}
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL);
cin >> N >> M;
solve(0);
return 0;
}
풀이 2
#include <bits/stdc++.h>
using namespace std;
int N, M;
int arr[10];
int isused[10];
void solve(int k)
{
if (k == M) {
for (int i = 0; i < M; i++)
cout << arr[i] << ' ';
cout << '\n';
return ;
}
int st = 1;
if (k != 0)
st = arr[k - 1];
for (int i = st; i <= N; i++)
{
arr[k] = i;
solve(k + 1);
}
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL);
cin >> N >> M;
solve(0);
return 0;
}
- 중복이 허용되고, 비내림차순이어야 한다. 비내림차순이라는 것은 k + 1번째 수가 k번째 수와 같거나 큰 수열이다. N과 M (2)와 거의 동일한데 오름차순인지, 비내림차순인지의 차이가 있다.
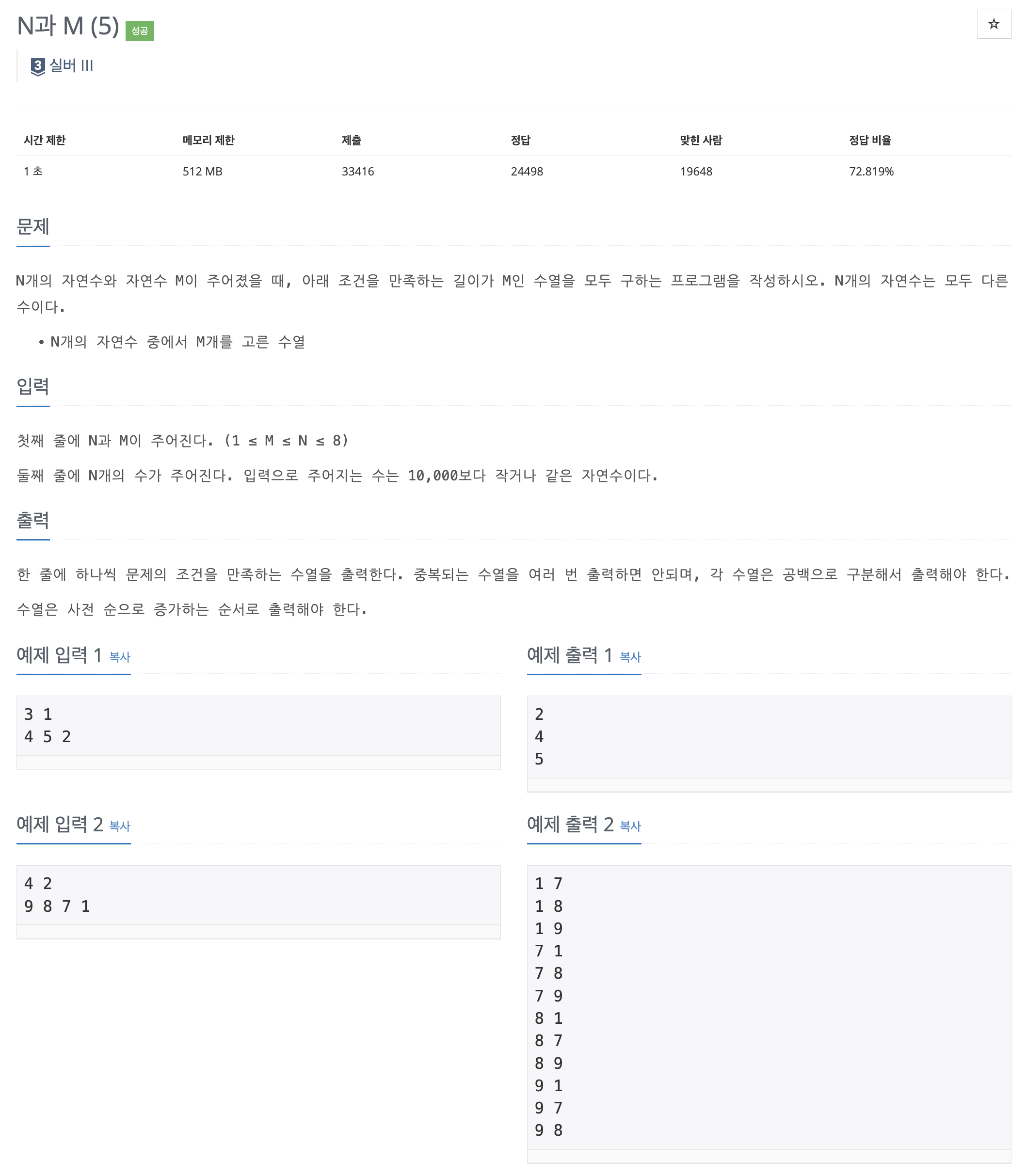
BOJ 15654, N과 M (5)
#include <bits/stdc++.h>
using namespace std;
int N, M;
vector<int> v;
int arr[10];
int isused[10];
void solve(int k)
{
if (k == M) {
for (int i = 0; i < M; i++)
cout << arr[i] << ' ';
cout << '\n';
return ;
}
for (int i = 0; i < N; i++) {
if (!isused[i]) {
arr[k] = v[i];
isused[i] = 1;
solve(k + 1);
isused[i] = 0;
}
}
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL);
cin >> N >> M;
for (int i = 0; i < N; i++) {
int num; cin >> num;
v.push_back(num);
}
sort(v.begin(), v.end());
solve(0);
return 0;
}
- N과 M (1)과 완전히 동일하지만, 따로 수열이 주어지기 때문에 arr[]에 처음부터 주어진 배열을 할당하거나 출력할 때 인덱스를 주거나 해야 한다. 마찬가지로 N과 M (6), (7), (8)은 (2), (3), (4)와 완전히 동일한 유형의 문제이기 때문에 넘어간다.
BOJ 15663, N과 M (9)
#include <bits/stdc++.h>
using namespace std;
int N, M;
int arr[10];
int isused[10];
vector<int> v;
// 1 7 9 9
void solve(int k)
{
if (k == M) {
for (int i = 0; i < M; i++)
cout << arr[i] << ' ';
cout << '\n';
return ;
}
int tmp = 0;
for (int i = 0; i < N; i++) {
if (!isused[i] && tmp != v[i]) {
arr[k] = v[i];
isused[i] = 1;
tmp = arr[k];
solve(k + 1);
isused[i] = 0;
}
}
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL);
cin >> N >> M;
for (int i = 0; i < N; i++) {
int num; cin >> num;
v.push_back(num);
}
sort(v.begin(), v.end());
solve(0);
return 0;
}
- 중복되는 수가 포함된 수열이 주어지는데, 중복되는 수열을 여러 번 출력하면 안된다. 이걸 어떻게 처리해야 할 지가 곤란스럽다. 결론적으로 말하자면 임시 int 변수에 배열의 마지막 수를 저장하고, 다음 인덱스의 수와 임시 변수를 비교하면 된다.
int tmp = 0; // 1) 임시 변수를 만든다
for (int i = 0; i < N; i++) {
if (!isused[i] && tmp != v[i]) {
// 3) 조건에 현재 수열의 수가 배열의 마지막 수와 같은지도 포함한다.
arr[k] = v[i];
isused[i] = 1;
tmp = arr[k]; // 2) 배열의 마지막 수를 임시 변수에 저장한다
solve(k + 1);
isused[i] = 0;
}
}
- 이렇게 하면 재귀가 어느 정도까지 파고들었는가와 관계없이 깔끔하게 중복되는 수열을 걸러낼 수가 있다. 이런 씽크빅이 있었을 줄이야…
BOJ 6603, 로또
#include <bits/stdc++.h>
using namespace std;
int K;
int arr[10];
int isused[10];
int num[10];
void solve(int k)
{
if (k == 6) {
for (int i = 0; i < 6; i++)
cout << arr[i] << ' ';
cout << '\n';
return ;
}
for (int i = 0; i < K; i++) {
if (!isused[i]) {
arr[k] = num[i];
if (k > 0 && arr[k - 1] > arr[k])
continue;
isused[i] = 1;
solve(k + 1);
isused[i] = 0;
}
}
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL);
while (1)
{
cin >> K;
if (K == 0)
break ;
for (int i = 0; i < K; i++) {
int t; cin >> t;
num[i] = t;
}
solve(0);
cout << '\n';
for (int i = 0; i < 10; i++) {
arr[i] = 0;
num[i] = 0;
}
}
return 0;
}
- 앞에서 풀었던 N과 M 유형에서 중복을 체크하는 isused 배열, 그리고 오름차순이 아닌 배열을 배제하는 조건식을 넣어 문제에서 요구하는 조건을 맞추었다.
for (int i = 0; i < K; i++) {
if (!isused[i]) {
arr[k] = num[i];
if (k > 0 && arr[k - 1] > arr[k])
continue;
isused[i] = 1;
solve(k + 1);
isused[i] = 0;
}
}
- 사실상 N과 M 문제의 연장선이 아닌지…
