BOJ 16985 - Maaaaaaaaaze

09 Apr 2024 in Posts on Random, CPP

“3차원 BFS를 이용한 시뮬레이션”

BOJ 16985 - Maaaaaaaaaze
- 문제 링크

BOJ 16985 - Maaaaaaaaaze

문제 링크

#include <bits/stdc++.h>
#define all(x) (x).begin(), (x).end()
#define rep(i, a, b) for (int i = (a); i < (b); ++i)
const int INF = 0x3f3f3f3f;
using namespace std;

int b[5][5][5];
int co[5][5][5];
vector<pair<int,int>>st(5);
int s_isused[10];
int dz[6] = {0, 0, 0, 0, 1, -1};
int dx[6] = {0, 0, 1, -1, 0, 0};
int dy[6] = {1, -1, 0, 0, 0, 0};
int dis[5][5][5];
vector<int>answers;
int t;

void    bfs()
{
    for (int i = 0; i < 5; i++) {
        for (int j = 0; j < 5; j++) {
            for (int k = 0; k < 5; k++)
                dis[i][j][k] = -1;
        }
    }
    if (co[0][0][0] == 0 || co[4][4][4] == 0)
        return ;
    queue<tuple<int,int,int>> q;
    q.push({0, 0, 0});
    dis[0][0][0] = 0;
    while (!q.empty())
    {
        tuple<int,int,int>cur = q.front(); q.pop();
        int cz = get<0>(cur);
        int cx = get<1>(cur);
        int cy = get<2>(cur);
        if (cz == 4 && cx == 4 && cy == 4) {
            int ans = dis[4][4][4];
            answers.push_back(ans);
            if (ans == 12)
                t = ans;
            return ;
        }
        for (int dir = 0; dir < 6; dir++) {
            int nz = cz + dz[dir];
            int nx = cx + dx[dir];
            int ny = cy + dy[dir];
            if (nx < 0 || nx > 4 || ny < 0 || ny > 4 || nz < 0 || nz > 4) continue;
            if (dis[nz][nx][ny] != -1 || co[nz][nx][ny] == 0) continue;
            dis[nz][nx][ny] = dis[cz][cx][cy] + 1;
            q.push({nz,nx,ny});
        }
    }
}

void    copy() 
{
    for (int i = 0; i <= 4; i++) {
        if (st[i].second == 0) {
            int cur = st[i].first;
            for (int r = 0; r < 5; r++) {
                for (int c = 0; c < 5; c++) {
                    co[i][r][c] = b[cur][r][c];
                }
            }
        }
        else if (st[i].second == 1) { // 90
            int cur = st[i].first;
            for (int r = 0; r < 5; r++) {
                for (int c = 0; c < 5; c++) {
                    co[i][r][c] = b[cur][c][4 - r];
                }
            }
        }
        else if (st[i].second == 2) { // 180
            int cur = st[i].first;
            for (int r = 0; r < 5; r++) {
                for (int c = 0; c < 5; c++) {
                    co[i][r][c] = b[cur][4 - r][4 - c];
                }
            }
        }
        else if (st[i].second == 3) { // 270
            int cur = st[i].first;
            for (int r = 0; r < 5; r++) {
                for (int c = 0; c < 5; c++) {
                    co[i][r][c] = b[cur][4 - c][r];
                }
            }
        }
    }
}

void    solve(int k)
{
    if (t == 12)
        return ;
    if (k == 5) {
        copy();
        bfs();
        return ;
    }

    for (int i = 0; i <= 3; i++) {
        st[k].second = i;
        solve(k + 1);
    }
}

void    force(int k)
{
    if (t == 12)
        return ;

    if (k == 5) {
        solve(0);
        return ;
    }

    for (int i = 0; i < 5; i++) {
        if (!s_isused[i]) {
            st[k].first = i;
            s_isused[i] = 1;
            force(k + 1);
            s_isused[i] = 0;
        }
    }
}

int main()
{
    ios_base::sync_with_stdio(false);
    cin.tie(NULL); cout.tie(NULL);

    for (int i = 0; i < 5; i++)
        for (int j = 0; j < 5; j++)
            for (int k = 0; k < 5; k++)
                cin >> b[i][j][k];
    force(0);
    if (answers.empty())
        cout << -1;
    else {
        sort(answers.begin(), answers.end());
        cout << answers[0] << '\n';
    }
    return 0;
}

딱봐도 엄청 풀기 싫게 생긴 외관 만큼이나 압도적인 길이를 자랑하는 풀이이다. 바로 이전 문제인 puyo puyo도 길다고 느꼈는데 이건 그거보다도 더 길었다…
결론적으로 말하면 이 문제는, 5*5*5인 3차원 배열에 대해 3차원 BFS를 사용하되, 모든 경우의 수를 탐색하는 완전 탐색 문제이다.
완전 탐색 문제는 풀이를 생각해내는 것보다도, 이 문제가 완전 탐색 문제인지 확신하는 것이 어려운 것 같다. 사실 이 문제의 연산량은 아무리 빡빡하게 잡아도 탑을 쌓는 경우 120가지와 탑을 돌리는 경우 4의 5승, 그리고 BFS의 O(N)(125)까지 해서 120 * 1024 * 125 = 15360000 정도인데, 이 정도면 충분히 완전 탐색이 가능한 범위인데도 지레 겁을 집어먹고 아무것도 못하고 2시간을 날려보냈다.
대략적인 절차는 구현에 따라 달라지겠지만 본인의 경우 탑을 먼저 쌓고, 쌓은 탑을 돌려가며 모든 경우의 이동 경로의 이동 수를 측정하면서 최소 경우인 12가 나오면 즉시 출력하고 종료하며 그렇지 않다면 경로들을 모아두었다가 제일 작은 이동 수를 출력하며 종료한다. 만약 도착 지점으로 가는 경로가 존재하지 않는다면 -1을 출력한다.
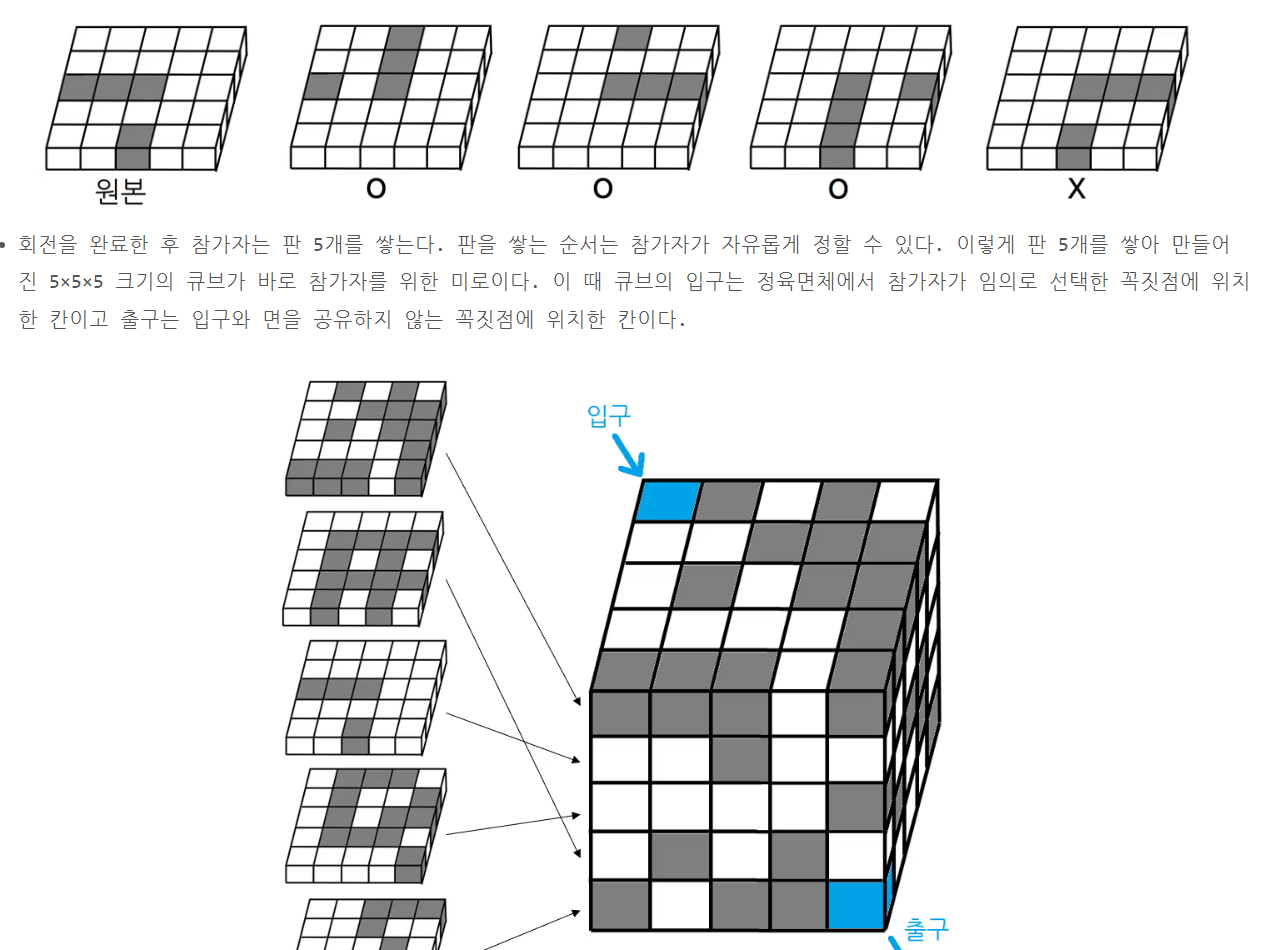
아래와 같이 탑을 쌓았다. force() 함수는 N과 M의 풀이를 적용한, 백트래킹으로 조합을 만드는 함수이다.

vector<pair<int,int>>st(5);
// st.first에 탑을 쌓는 경우의 수 배열이 저장된다.

void    force(int k)
{
    if (t == 12)
        return ;

    if (k == 5) {
        // st.first 배열
        // 1 2 3 4 5
        // 1 2 3 5 4
        // ...
        // ...
        // 5 4 3 2 1 
        solve(0);
        return ;
    }

    for (int i = 0; i < 5; i++) {
        if (!s_isused[i]) {
            st[k].first = i;
            s_isused[i] = 1;
            force(k + 1);
            s_isused[i] = 0;
        }
    }
}

곧바로 이어지는 solve() 함수는, 탑을 돌리는 순열을 만드는 함수이다. force 함수와 동일한 구조를 갖고 있다.

vector<pair<int,int>>st(5);
// st.first에 탑을 쌓는 경우의 수 배열이 저장된다.
// st.second에 탑을 돌리는 경우의 수 배열이 저장된다.
// 0 -> 회전 X, 1 -> 90도 회전, 2 -> 180도 회전, 3 -> 270도 회전

void    solve(int k)
{
    if (t == 12)
        return ;
    
    if (k == 5) {
        // st.second 배열
        // 0 0 0 0 0
        // 0 0 0 0 1
        // 0 0 0 0 2
        // ...
        // ...
        // 3 3 3 3 3
        copy();
        bfs();
        return ;
    }

    for (int i = 0; i <= 3; i++) {
        st[k].second = i;
        solve(k + 1);
    }
}

copy 함수는 원본 배열 b를 새로운 배열 co에 옮겨담되, st 배열의 first와 second를 참조하여 적절한 순서와, 적절한 각도로 옮겨담는다. 여기서 실수를 하면 문제를 푸는데 애로사항이 생기게 된다…

void    copy() 
{
    for (int i = 0; i <= 4; i++) {
        if (st[i].second == 0) {
            int cur = st[i].first;
            for (int r = 0; r < 5; r++) {
                for (int c = 0; c < 5; c++) {
                    co[i][r][c] = b[cur][r][c];
                }
            }
        }
        else if (st[i].second == 1) { // 90도
            int cur = st[i].first;
            for (int r = 0; r < 5; r++) {
                for (int c = 0; c < 5; c++) {
                    co[i][r][c] = b[cur][c][4 - r];
                }
            }
        }
        else if (st[i].second == 2) { // 180도
            int cur = st[i].first;
            for (int r = 0; r < 5; r++) {
                for (int c = 0; c < 5; c++) {
                    co[i][r][c] = b[cur][4 - r][4 - c];
                }
            }
        }
        else if (st[i].second == 3) { // 270도
            int cur = st[i].first;
            for (int r = 0; r < 5; r++) {
                for (int c = 0; c < 5; c++) {
                    co[i][r][c] = b[cur][4 - c][r];
                }
            }
        }
    }
}

각도에 따라 r, c를 조정하여 옮기는데, 이 부분은 구글 선생님의 도움을 좀 받았다…
탑이 완성되었으므로, bfs를 돌며 경로의 이동 수를 측정한다. 3차원 BFS를 돌 줄 안다면 쉽게 작성할 수 있는 함수이다.

void    bfs()
{
    for (int i = 0; i < 5; i++) {
        for (int j = 0; j < 5; j++) {
            for (int k = 0; k < 5; k++)
                dis[i][j][k] = -1;
        }
    }

    if (co[0][0][0] == 0 || co[4][4][4] == 0)
        return ;
    
    queue<tuple<int,int,int>> q;
    q.push({0, 0, 0});
    dis[0][0][0] = 0;
    
    while (!q.empty())
    {
        tuple<int,int,int>cur = q.front(); q.pop();
        int cz = get<0>(cur);
        int cx = get<1>(cur);
        int cy = get<2>(cur);
        
        if (cz == 4 && cx == 4 && cy == 4) {
            int ans = dis[4][4][4];
            answers.push_back(ans);
            if (ans == 12)
                t = ans;
            return ;
        }
        
        for (int dir = 0; dir < 6; dir++) {
            int nz = cz + dz[dir];
            int nx = cx + dx[dir];
            int ny = cy + dy[dir];
            if (nx < 0 || nx > 4 || ny < 0 || ny > 4 || nz < 0 || nz > 4) 
                continue;
            if (dis[nz][nx][ny] != -1 || co[nz][nx][ny] == 0) 
                continue;
            dis[nz][nx][ny] = dis[cz][cx][cy] + 1;
            q.push({nz,nx,ny});
        }
    }
}

BOJ 16985 - Maaaaaaaaaze

BOJ 16985 - Maaaaaaaaaze

문제 링크

나는 gyopark

Error

BOJ 16985 - Maaaaaaaaaze

문제 링크

Templates (for web app):

Error