BOJ 16987 - 계란으로 계란치기
“백트래킹”
BOJ 16987 - 계란으로 계란치기
문제 링크

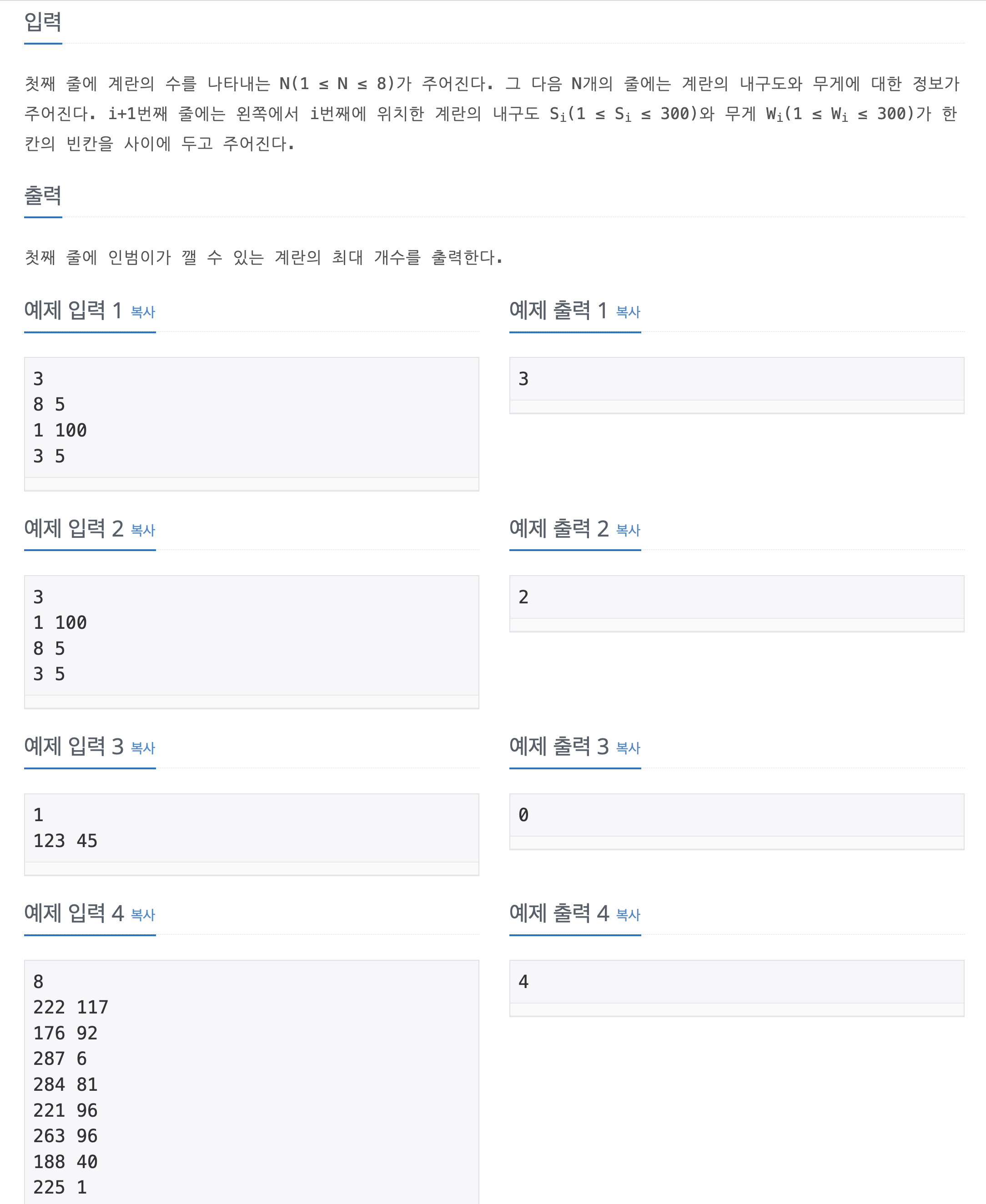
#include <bits/stdc++.h>
typedef long long ll;
const int INF = 0x3f3f3f3f;
using namespace std;
int N, ans;
vector<pair<int,int>> eggs;
void solve(int idx, int broken)
{
if (idx == N) {
ans = max(ans, broken);
return ;
}
if (eggs[idx].first <= 0) {
solve(idx + 1, broken);
} else {
bool hit = false;
for (int i = 0; i < N; i++) {
if (i != idx && eggs[i].first > 0) {
hit = true;
eggs[idx].first -= eggs[i].second;
eggs[i].first -= eggs[idx].second;
int nbroken = broken + (eggs[idx].first <= 0) + (eggs[i].first <= 0);
solve(idx + 1, nbroken);
eggs[idx].first += eggs[i].second;
eggs[i].first += eggs[idx].second;
}
}
if (!hit) {
solve(idx + 1, broken);
}
}
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL); std::cout.tie(NULL);
cin >> N;
eggs.resize(N);
for (int i = 0; i < N; i++) {
cin >> eggs[i].first >> eggs[i].second;
}
solve(0, 0);
cout << ans << '\n';
return 0;
}
생각해낸다고 치면 생각해내기가 그렇게 어렵지 않았을지 모를 백트래킹 문제라고 여겼는데, 결국 생각해내지 못하고 chatGPT의 도움을 받아버리고 말았다. 아주 기똥차게 짜주더라…
아래의 코드는 원래 내가 짰던 코드이다. 문제가 아주 많기 때문에 찌피티의 해설을 기반하여 정답 코드와 비교하며 복기해보고자 한다…
int N;
vector<tuple<int,int,bool>> vp;
int ans = 0;
void solve(int k)
{
if (k == N) {
return ;
}
// get<0>->내구도, get<1>->무게, get<2>->깨졌는지여부
int p = INF;
int cd = get<0>(vp[k]); int cw = get<1>(vp[k]); int cb = get<2>(vp[k]);
for (int i = 0; i < N; i++)
{
if (i == k)
continue ;
if (!get<2>(vp[i])) {
p = i;
break ;
}
}
int pd, pw, pb;
if (cb || p == INF)
;
else
{
int pd = get<0>(vp[p]); int pw = get<1>(vp[p]); int pb = get<2>(vp[p]);
cout << k << "번째 계란 vs " << p << "번째 계란\n";
int ncd = cd - pw;
int npd = pd - cw;
if (ncd < 0) {
cout << "-- k계란이 깨짐 --\n";
ans += 1;
}
if (npd < 0) {
cout << "-- pick계란이 깨짐 --\n";
ans += 1;
}
vp[k] = make_tuple(ncd, cw, true);
vp[p] = make_tuple(npd, pw, true);
}
solve(k+1);
vp[k] = make_tuple(cd, cw, false);
if (p != INF)
vp[p] = make_tuple(pd, pw, false);
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL); std::cout.tie(NULL);
cin >> N;
for (int i = 0; i < N; i++) {
int d, w; cin >> d >> w;
vp.push_back({d, w, false}); // false 안 깨졌다는 뜻
}
solve(0);
cout << ans;
return 0;
}
- 살펴볼 점은 아래와 같다.
(1) 상태 관리 및 복원
백트래킹의 정수라고도 볼 수 있다. 내가 작성했던 코드에서 현재 쥔 계란의 상태를 내구도/무게/깨진지 아닌지의 여부의 세 가지 요소로
int cd = get<0>(vp[k]); int cw = get<1>(vp[k]); int cb = get<2>(vp[k]);로, 깨고자 하는 계란의 상태를int pd = get<0>(vp[p]); int pw = get<1>(vp[p]); int pb = get<2>(vp[p]);로 나타내었는데, 해답 코드에서는 깨졌는지의 여부는 매개변수로 빼고, 내구도와 무게만 pair로 vector로 만들어 연산하였다.복원하는 절차의 경우, 내구도를 무게만큼 차감하였기 때문에 그대로 다시 올려주면 되고 깨진 계란의 수같은 경우 다음 재귀를 돌때 매개변수 자체를 건들지 않으면 손댈 필요 자체가 없는데 내가 원래 짠 코드의 경우 상태 관리에 깨졌는지 아닌지의 여부도 포함되어있고, 복원하는 논리도 이상했다. 찌피티가 코드를 잘짜기는 하는것 같다 ㅋㅋ;
(2) 깨진 계란 처리
eggs[idx].first -= eggs[i].second;
eggs[i].first -= eggs[idx].second;
- pair의 경우 이런식으로 값의 수정이 직접 반영되지만, tuple의 경우 이런 식으로 직접 반영하는 코드는 C++17 이후에 가능하다고 한다. tuple의 경우 내가 원래 작성한 코드처럼 value를 따로 빼서 다시 할당하는 작업을 거쳐야 한다. pair를 사용할 수 있다면 tuple 대신 pair를 사용하는 게 편리하긴 하겠다.
(3) 가능한 모든 경우 탐색
- 모든 경우의 수를 다 고려해보기 위해, 안 깨진 계란을 찾는 반복문이 필요한데 이 논리의 경우 원래 코드에도 포함되어 있다. 다만 상태 관리하는 요소가 다르기 때문에 정답 코드처럼 내구도 자체를 보는 것이 깨진 여부를 따로 판별하는 것보다 간단할 것 같다.
(4) 재귀 탐색
- 정답 코드의 경우, 다음 재귀로 넘어가는
solve(k + 1)이 내가 손에 쥔 계란이 깨진 경우 깨트릴 계란이 없는 경우로 엄밀하게 나누어져 있지만, 내 코드의 경우 그것이 섞여서 어물쩍 넘어가게 된다. 백트래킹 코드의 경우 분기를 엄밀하게 나누는 것이 좋겠다.
