BOJ 1753 - 최단경로
“다익스트라 알고리즘”
BOJ 1753 - 최단경로
문제 링크

#include <bits/stdc++.h>
typedef long long ll;
const int INF = 0x3f3f3f3f;
using namespace std;
int V, E;
int K;
vector<pair<int,int>> adj[20020];
int d[20020];
priority_queue<pair<int,int>,vector<pair<int,int>>,greater<pair<int,int>>> pq;
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL);
cin >> V >> E;
cin >> K;
for (int i = 0; i < E; i++) {
int u, v, w; cin>>u>>v>>w;
adj[u].push_back({w, v});
}
fill(d, d + V + 1, INF);
d[K] = 0;
pq.push({d[K], K}); // 거리, 정점
while (!pq.empty())
{
pair<int,int>cur = pq.top(); pq.pop();
// cur.first -> dist;
// cur.second -> node, d[cur.second] == cur.first;
// 정점에 해당하는 최소 거리가 아니라면 pop만 하고 continue
if (d[cur.second] != cur.first)
continue ;
for (int i = 0; i < adj[cur.second].size(); i++) {
pair<int,int>nxt = adj[cur.second][i];
// nxt.first -> dist;
// nxt.second -> node, d[nxt.second] == nxt.first;
if (d[nxt.second] > cur.first + nxt.first) {
d[nxt.second] = cur.first + nxt.first;
pq.push({d[nxt.second], nxt.second});
}
}
}
for (int i = 1; i <= V; i++) {
if (d[i] == INF)
cout << "INF\n";
else
cout << d[i] << '\n';
}
return 0;
}
다익스트라 알고리즘을 사용하여, 정점 1에서 나머지 정점으로 가는 가장 최단거리를 기록하여 출력하는 문제이다.
다익스트라 알고리즘은 우선순위 큐를 이용하여 구현할 수 있다. 각각의 정점과 거리를 쌍으로 묶어 우선순위 큐에 저장하며, 우선순위 큐는 거리를 기준으로 하는 최소 힙으로 구현되기 때문에 큐의 루트에는 항상 기준으로 하는 정점으로부터 가장 가까운 거리를 가지는 거리-정점 쌍이 위치하게 된다. 당면한 상황에서 항상 거리가 제일 짧은 정점만을 바라보기 때문에, 그리디한 속성을 가진다고도 볼 수 있다.
d[K] = 0;
pq.push({d[K], K}); // 거리, 정점
while (!pq.empty())
{
pair<int,int>cur = pq.top(); pq.pop();
// cur.first -> dist;
// cur.second -> node, d[cur.second] == cur.first;
// 정점에 해당하는 최소 거리가 아니라면 pop만 하고 continue
if (d[cur.second] != cur.first)
continue ;
for (int i = 0; i < adj[cur.second].size(); i++) {
pair<int,int>nxt = adj[cur.second][i];
// nxt.first -> dist;
// nxt.second -> node, d[nxt.second] == nxt.first;
if (d[nxt.second] > cur.first + nxt.first) {
d[nxt.second] = cur.first + nxt.first;
pq.push({d[nxt.second], nxt.second});
}
}
}
- 해당 부분이 다익스트라 알고리즘의 핵심이다.
(거리, 정점)으로 큐에 기록하기 때문에,cur을 큐에서 빼낼 때,cur.first가 거리이고,cur.second가 그 해당 노드임을 확인할 수 있다.d[505]는 기준 노드로부터 최소의 거리를 기록하는 거리 배열인데, 잘 생각해보면 d 배열이 최소의 거리를 가리킨다면d[cur.second] == cur.first가 성립한다는 것을 알 수가 있다. 애초에 저 while문이 그렇게 되도록 d 배열을 교정하는 반복문이다.
for (int i = 0; i < adj[cur.second].size(); i++) {
pair<int,int>nxt = adj[cur.second][i];
// nxt.first -> dist;
// nxt.second -> node, d[nxt.second] == nxt.first;
if (d[nxt.second] > cur.first + nxt.first) {
d[nxt.second] = cur.first + nxt.first;
pq.push({d[nxt.second], nxt.second});
}
}
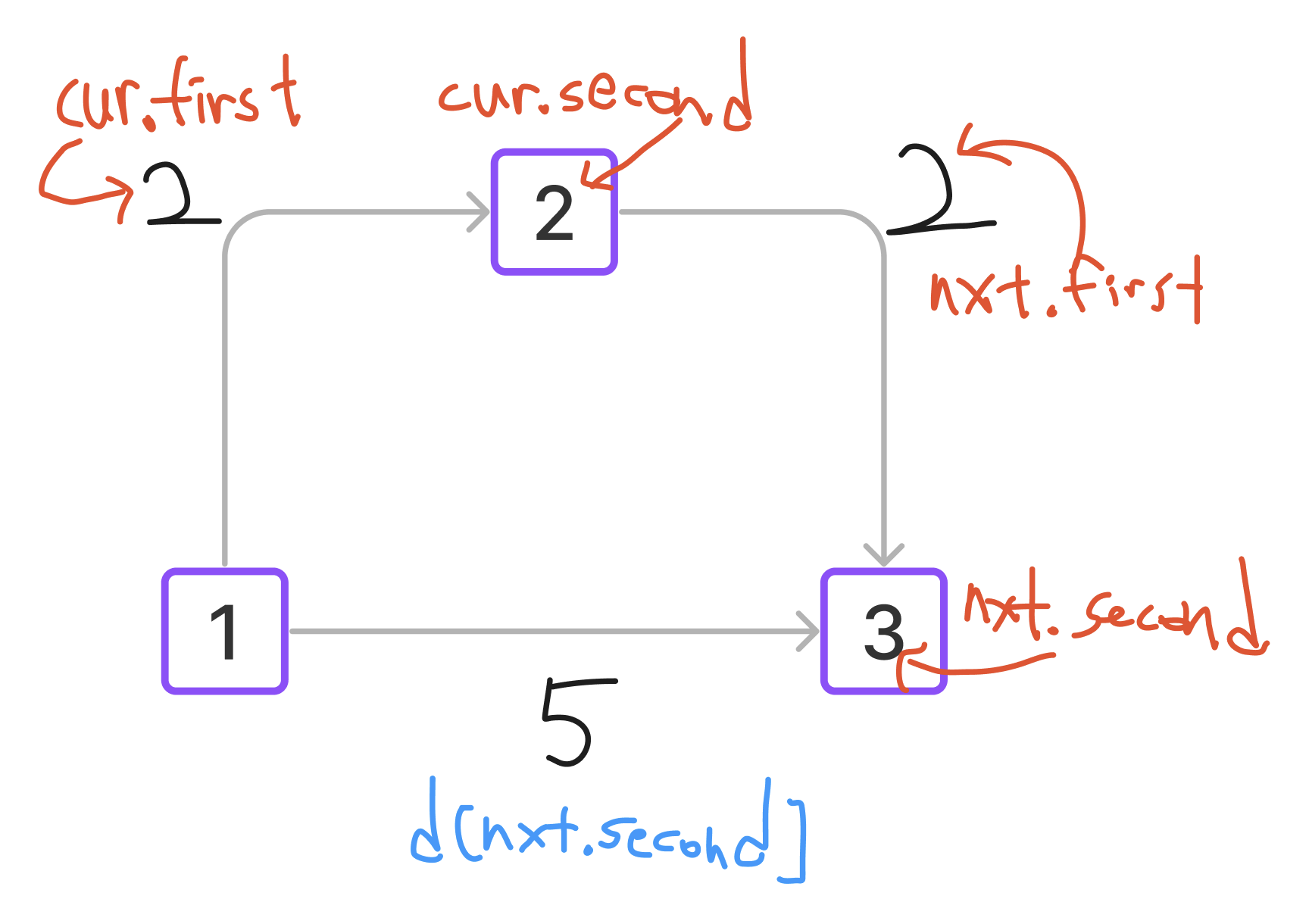
- 1에서 3으로 가는 최단 거리는 4지만, 처음에는 5로 기록되어 있을 것이다(d[3] = 5). 먼저 1에서 한번에 도달할 수 있는 방법인 5를 먼저 d 배열에 넣었기 때문이다. 그러나 1에서 2로 간 후, 2에서 3으로 가는 방법(d[2] + 2)이 기존의 d[3]보다 짧기 때문에, 이후의 반복문에서 d[3]이; d[2] + 2로 대체되는데, 위 코드는 그 과정이 담겨있다. 사실상 다익스트라 알고리즘의 정수라 볼 수 있다. 그림에서 푸른색 5인
d[nxt.second]가,cur.first+nxt.first인 4로 대체된다는 것을 확인할 수 있다.
