BOJ 2133 - 타일 채우기
“다이나믹 프로그래밍”
BOJ 2133 - 타일 채우기
문제 링크

#include <bits/stdc++.h>
#define all(x) (x).begin(), (x).end()
#define rep(i, a, b) for (int i = (a); i < (b); ++i)
const int INF = 0x3f3f3f3f;
using namespace std;
typedef long long ll;
int N;
ll dp[33];
int check(int k)
{
ll sum = 0;
ll st = k - 2;
for (int i = st; i >= 0; i -= 2)
{
if (i == st)
sum += dp[i] * 3;
else if (i == 0)
sum += 2;
else
sum += dp[i] * 2;
}
return sum;
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL);
cin >> N;
dp[1] = 0;
dp[2] = 3;
dp[3] = 0;
dp[4] = 11;
for (int i = 5; i <= N; i++) {
if (i % 2)
dp[i] = 0;
else
dp[i] = check(i);
}
cout << dp[N];
return 0;
}
여태까지 타일 채우기 문제들은 어떻게 그림판에 쓱쓱 그리면 점화식을 유도할 수가 있었는데, 이번엔 집중을 잘 못해서 그런가 경우의 수를 찾아내는데 어려움을 겪었다. 저기 힌트로 주어진 그림이 핵심이다.
우선
3 * N벽을 채울 때, N이 홀수면 벽을 채울 수 있는 경우의 수가 존재하지 않는다.3 * 1인 벽을 채울 수 없다는 것을 생각해보면 나머지 홀수 길이의 벽들을 채울 수 없다는 것을 짐작할 수가 있다.3 * 2벽을 세우는 경우는 아래의 3가지가 있다.
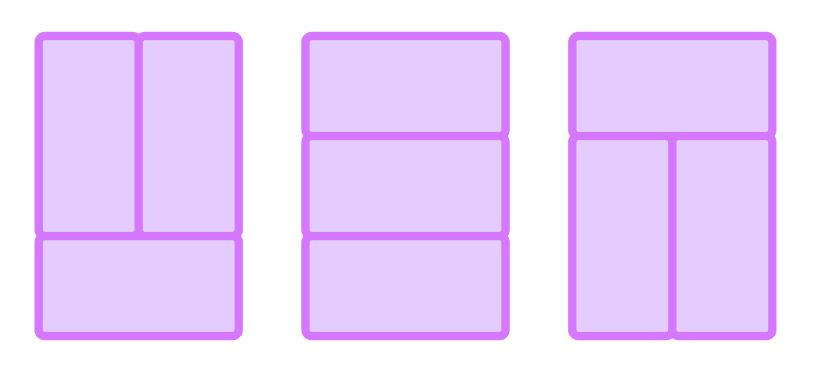
- 그렇다면,
3 * i를 채우는 경우의 수는 대략3 * (i - 2)을 채우는 경우의 수에 3을 곱하거나 하면 될 것 같다고 예상할 수가 있는데, 여기서 끝이 아니라 힌트에서 주어진 것과 같은 추가 경우의 수가 더 있다.3 * 4벽을 세우는 경우는3 * 2벽을 채우는 그림을 단순히 이어붙이는 형태 이외에도 힌트와 같은 형태가 더 있다.
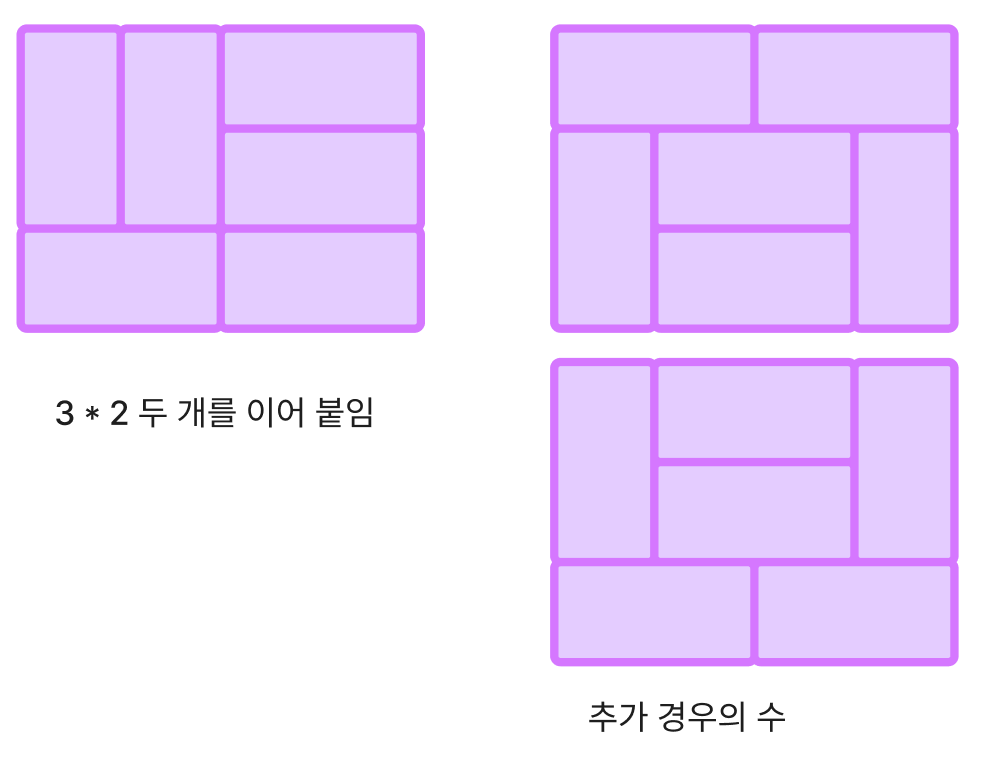
- 이런 새로운 형태의 경우의 수가 4 -> 6 -> 8 -> … 로 N이 2씩 증가할 때마다 새롭게 생겨나게 된다(2개씩). 나는 이걸 간과하고 추가적인 경우의 수를 자꾸 빠트렸다.
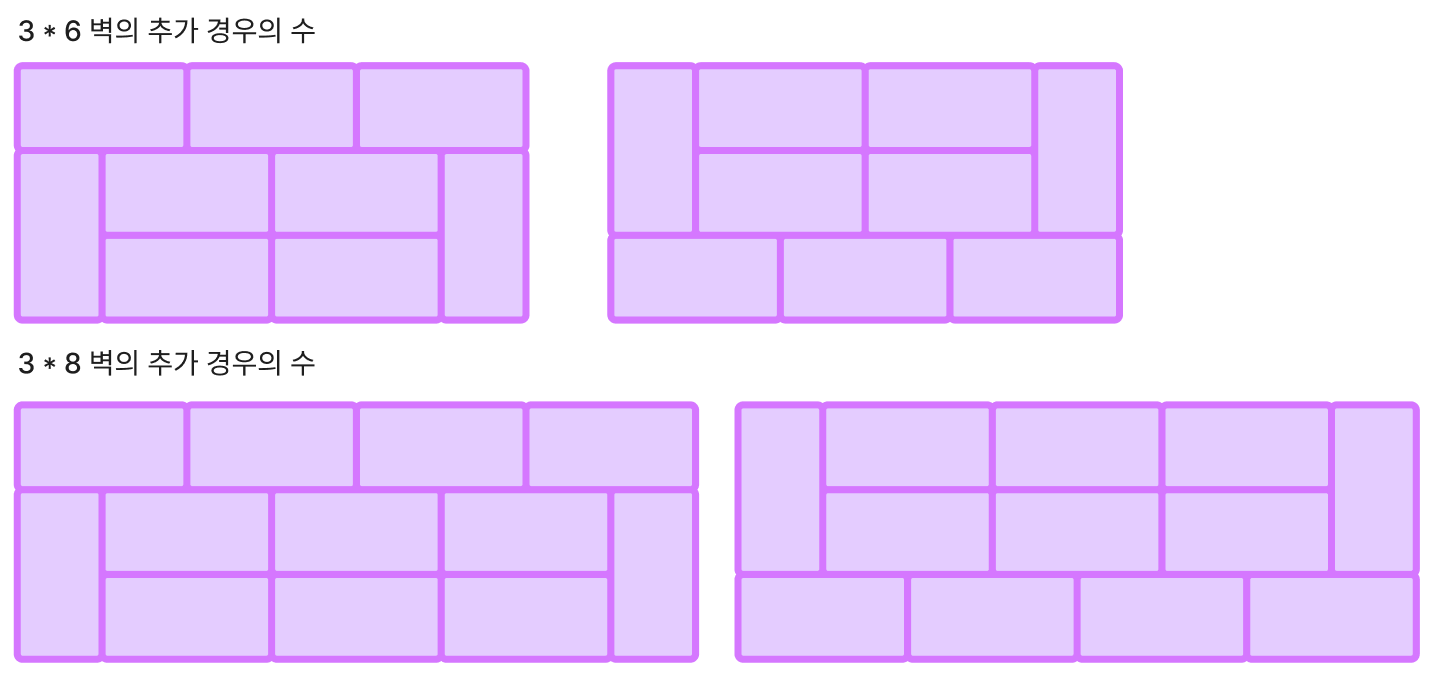
- 이러한 추가 경우의 수 때문에,
3 * i벽을 채울 때 단순히3 * (i - 2)의 개수에3 * 2의 세 가지만 곱하는 것이 아니라 여태까지 계산해온 모든 짝수 개의 추가 경우의 수까지 포함시켜서 경우를 찾아야 한다. 예를 들어3 * 6벽을 채우는 경우의 수를 찾는다고 한다면
(1) 먼저 3 * 4의 모든 경우의 수에 3(3 * 2의 경우의 수)을 곱한다.
(2) 1의 경우는 추가 경우의 수가 왼쪽에 있는 경우만 헤아린 것이기 때문에, 추가 경우의 수가 오른쪽에 오게 되는 경우도 세야 한다. 이것은 여태까지 지나온 짝수 dp의 경우에 2를 곱하는 것으로 셀 수가 있다.
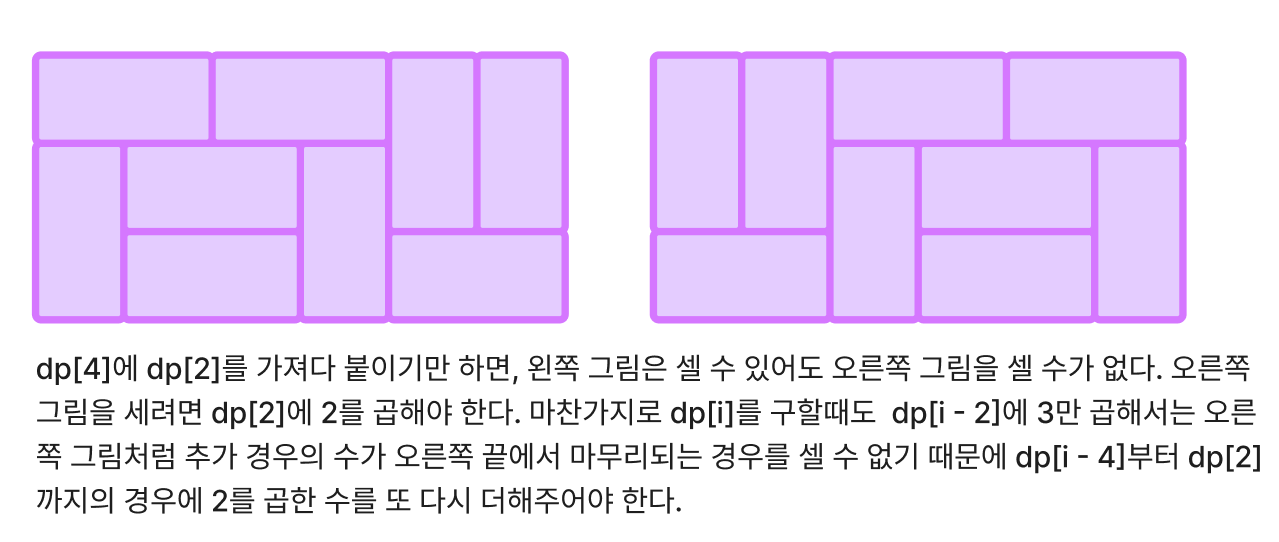
(3) 마지막으로 추가 경우의 수 2를 더한다.
- 이것을 토대로 점화식을 세우면 아래와 같다.
dp[i] = dp[i - 2] * 3 + (dp[i - 4] * 2 + ... + dp[0] * 2) + 2;
- 그것의 구현부가 아래이다.
int check(int k)
{
ll sum = 0;
ll st = k - 2;
for (int i = st; i >= 0; i -= 2)
{
if (i == st)
sum += dp[i] * 3;
else if (i == 0)
sum += 2;
else
sum += dp[i] * 2;
}
return sum;
}
