BOJ 2156 - 포도주 시식, 2579 - 계단 오르기
“다이나믹 프로그래밍”
BOJ 2156 - 포도주 시식, 2579 - 계단 오르기

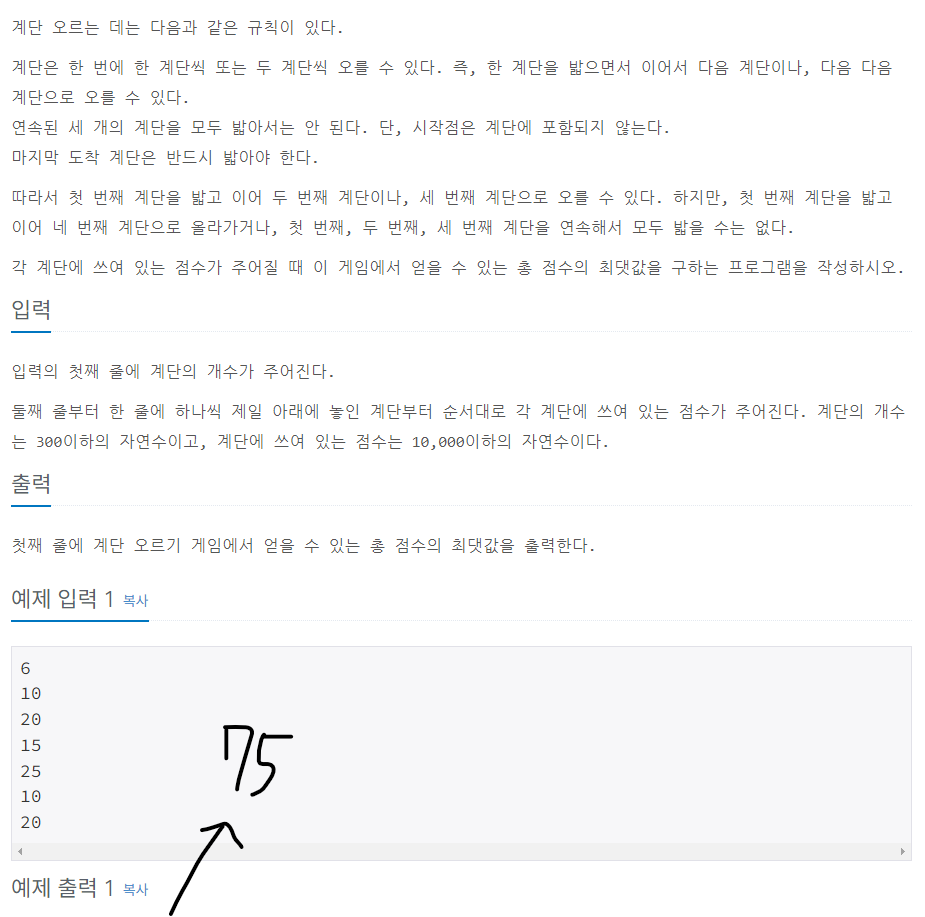
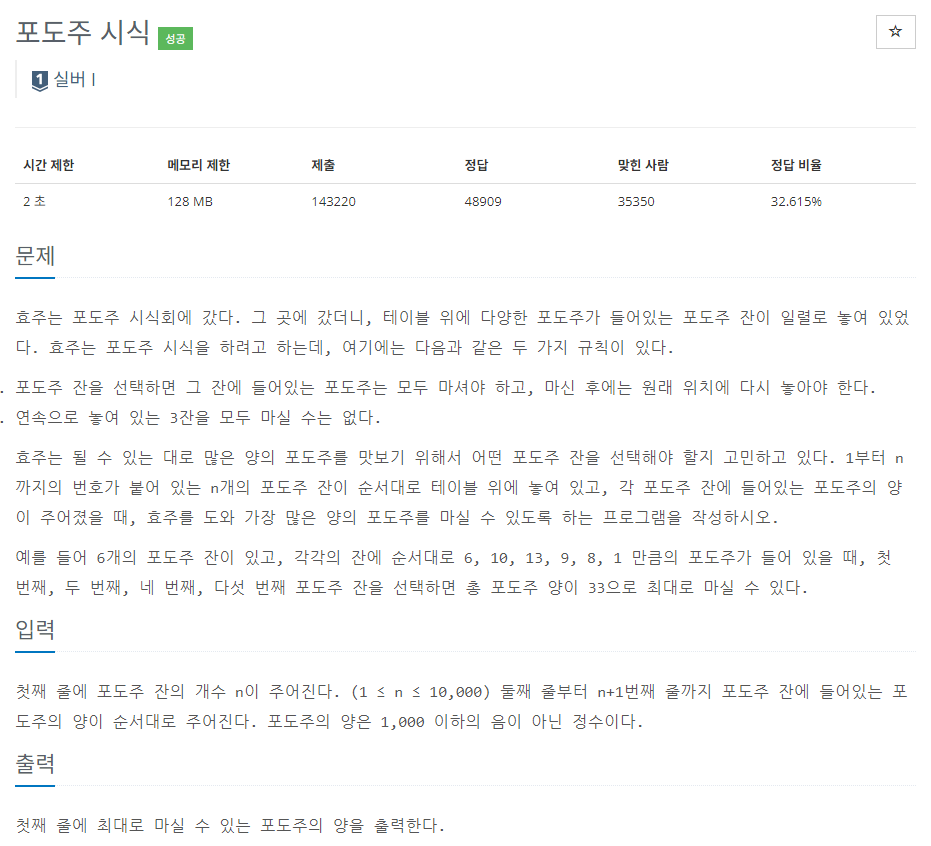
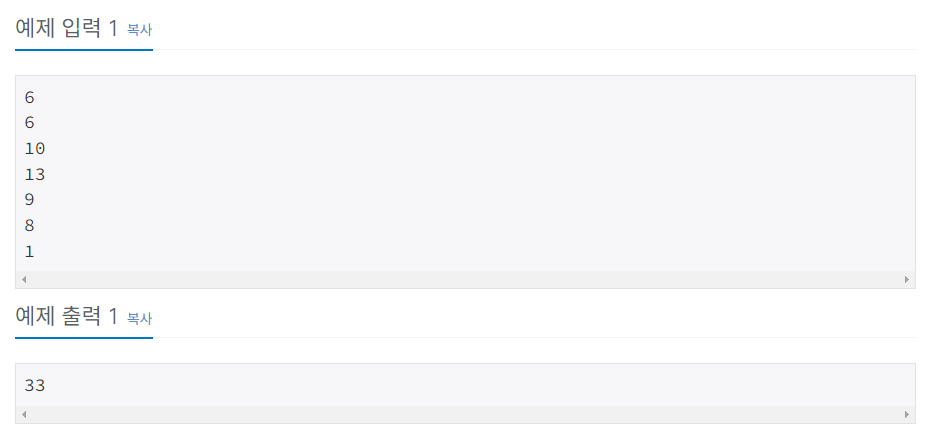
계단 오르기
#include <bits/stdc++.h>
#define all(x) (x).begin(), (x).end()
#define rep(i, a, b) for (int i = (a); i < (b); ++i)
const int INF = 0x3f3f3f3f;
using namespace std;
int N;
int arr[303];
int dp[303];
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL);
cin >> N;
for (int i = 1; i <= N; i++)
cin >> arr[i];
dp[1] = arr[1];
for (int i = 2; i <= N; i++) {
dp[i] = max(dp[i - 2] + arr[i], dp[i - 3] + arr[i - 1] + arr[i]);
}
cout << dp[N];
return 0;
}
포도주 시식
#include <bits/stdc++.h>
#define all(x) (x).begin(), (x).end()
#define rep(i, a, b) for (int i = (a); i < (b); ++i)
const int INF = 0x3f3f3f3f;
using namespace std;
int N;
int arr[10101];
int dp[10101];
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL);
cin >> N;
for (int i = 1; i <= N; i++) {
cin >> arr[i];
}
dp[1] = arr[1];
dp[2] = arr[1] + arr[2];
for (int i = 3; i <= N; i++) {
dp[i] = max(max(dp[i - 3] + arr[i - 1]+ arr[i], dp[i - 2] + arr[i]), dp[i - 1]);
}
cout << dp[N];
return 0;
}
두 문제의 경우 풀이가 거의 비슷하다. 다만 점화식을 세울 때 접근하는 방식에 약간의 차이가 있다.
포도주 시식의 경우 i번째 선택에서의 최댓값을 구할 때 i번째 포도주를 마시지 않을 수가 있지만, 계단 오르기의 경우 i번째 계단에서의 최댓값을 구한다고 가정했을 때, 반드시 i번째 계단에 올라서야 한다는 점에 차이가 있다.
i가 3이고, 각각의 값이
4 3 2라고 했을 때 포도주를 마시는 경우는 아래와 같다.
✔✔
4 3 2 -> 최댓값 dp[3] = 7, 마지막 포도주를 마시지 않아도 되기 때문에 생기는 경우의 수
✔ ✔
4 3 2 -> 후보 dp[i] = 6, i-2 번째 잔을 마시고 한 잔 걸러 i번째 잔을 마시는 경우
✔ ✔
4 3 2 -> 후보 dp[i] = 5, i-1 번째 잔을 마시고 연속으로 i번째 잔을 마시는 경우
- 세 번째 선택에, 세 번째 포도주를 마시지 않아도 되기 때문에 첫 번째 경우인 7이 최댓값이 된다. 포도주 시식의 점화식은 아래 세 가지 경우를 고려하게 된다.
(1) dp[i - 1]
-> 마지막 포도주를 마시지 않아도 되기 때문에 생기는 경우의 수
i-1 번째 잔까지 마셨을 때의 최댓값이 그대로 이어진다.
(2) dp[i - 2] + arr[i]
-> i-2 번째 잔까지 마셨을 때의 최댓값 + i번째 잔을 마셨을 때의 값
(3) dp[i - 3] + arr[i - 1] + arr[i]
-> 연속으로 세 번 포도주를 마실 수가 없기 때문에, i-1번째 잔과 i번째 잔을 마셨다면
i-3 번째 잔까지 마셨을 때의 최댓값에 더해주게 될 것이다.
// 점화식
for (int i = 3; i <= N; i++)
dp[i] = max({dp[i - 3] + arr[i - 1]+ arr[i], dp[i - 2] + arr[i], dp[i - 1]});
- i가 3개이고, 각각의 값이
4 3 2라고 했을 때 계단을 오르는 경우는 아래와 같다.
✔ ✔
4 3 2 -> 최댓값 dp[i] = 6
✔ ✔
4 3 2 -> 후보 dp[i] = 5
- 세 번째 계단(마지막 계단)을 반드시 밟아야 한다는 제한 조건이 생겼기 때문에, 4와 3을 오르고 마지막 계단을 건너뛰는 경우의 수는 고려할 수가 없다. 계단 오르기의 점화식은 아래 두 가지 경우를 고려하게 된다.
- 마지막 계단을 밟지 않는 경우의 수인 dp[i - 1]은 경우에서 제외되고, 두 가지 경우의 수만을 비교한다.
(1) dp[i - 2] + arr[i]
-> i-2번째 계단까지의 최댓값 + 두 칸 뛰어 마지막 계단 arr[i]의 값을 합한 value
(2) dp[i - 3] + arr[i - 1] + arr[i]
-> i-3번째 계단까지의 최댓값 + 두 칸 뛰어 i-1번째 계단 오르고 연속으로 하나 더 오른
마지막 계단 arr[i]의 값을 합한 value
// 점화식
for (int i = 2; i <= N; i++)
dp[i] = max(dp[i - 2] + arr[i], dp[i - 3] + arr[i - 1] + arr[i]);
- 이는 마지막 계단 i가 3보다 더 큰 수가 되어도 항상 유효하다. 매 선택마다 항상 마지막 계단을 밟아야 한다는 사실을 동일하기 때문이다.
