BOJ 26084 - DPS
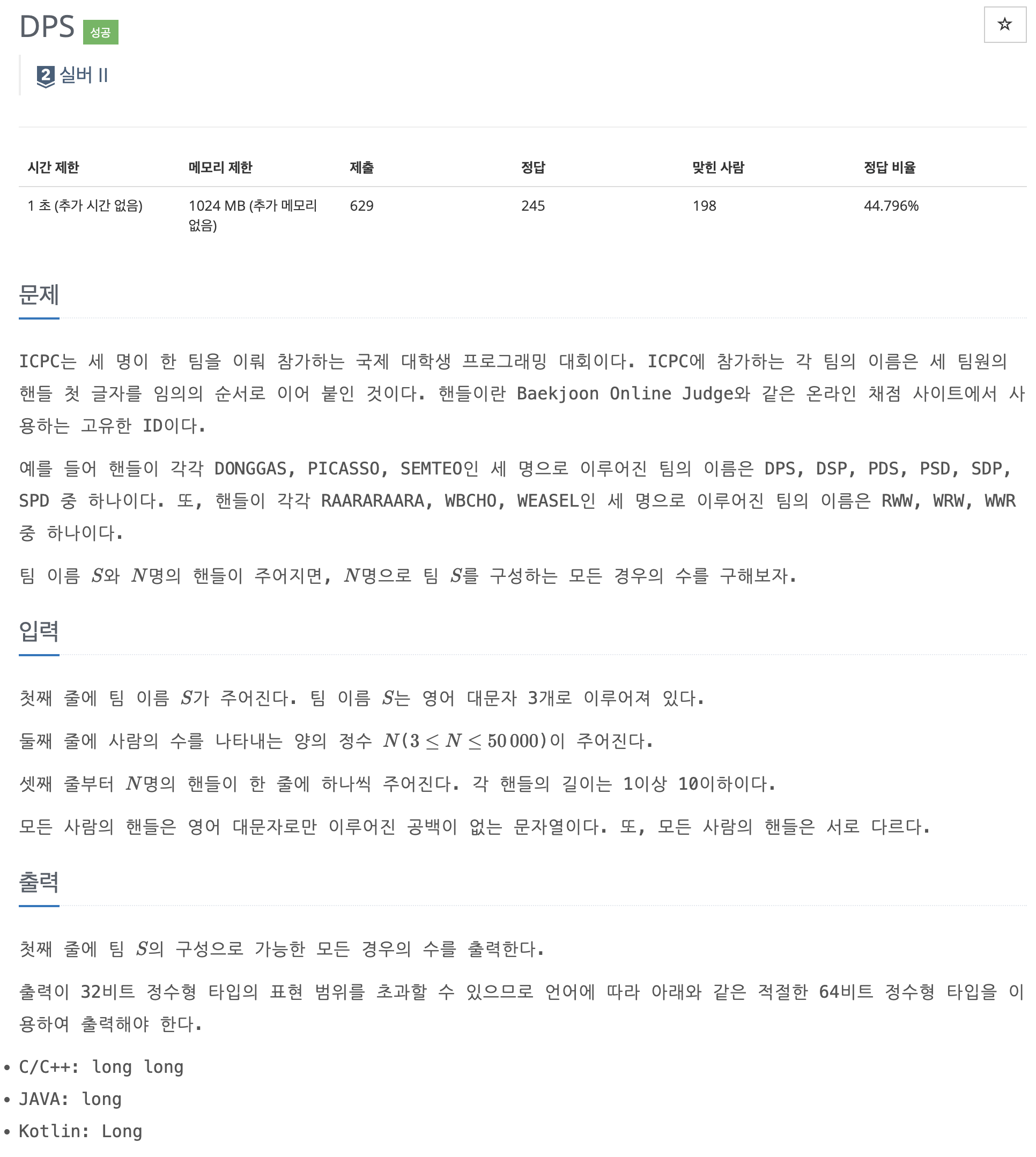
문제 링크

CODE
#include <bits/stdc++.h>
#define all(x) (x).begin(), (x).end()
#define rep(i, a, b) for (int i = (a); i < (b); ++i)
typedef long long ll;
const int INF = 0x3f3f3f3f;
using namespace std;
string S;
ll N;
ll karr[26];
ll narr[26];
ll ans = 1;
ll comb(int n, int k)
{
ll dp[n + 1][k + 1];
for (int i = 0; i <= n; i++)
fill(dp[i], dp[i] + k, 0);
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= min(i, k); j++) {
if (j == 0 || j == i) {
dp[i][j] = 1;
}
else {
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
}
}
}
return dp[n][k];
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL); std::cout.tie(NULL);
cin >> S >> N;
// 팀네임 알파벳 파악
for (int i = 0; i < S.length(); i++)
karr[(int)S[i] - 65]++;
// 팀원들 이름의 첫 알파벳 파악
for (int i = 0; i < N; i++) {
string s; cin >> s;
narr[(int)s[0] - 65]++;
}
bool check = true;
for (int i = 0; i < 26; i++) {
// 두 개가 겹치는 경우 가능한 조합을 곱한다.
if (karr[i] != 0 && narr[i] != 0) {
ans *= comb(narr[i], karr[i]);
}
// 만들어야 할 알파벳이 팀원들의 이름에 존재하지 않는다면
// 애초에 만들 수 있는 경우의 수가 존재하지 않는다.
if (karr[i] != 0 && narr[i] == 0)
check = false;
}
if (check)
cout << ans;
else
cout << 0;
return 0;
}
DESCRIPTION
조합에 대해 알고 있다면 수월하게 풀 수 있다. 특히 두 정수 $n,k$가 주어졌을 때, $O(NK)$로 $_nC_k$를 반환받는 함수를 만들 수 있어야 한다.
사실 팀원의 구체적인 이름이 무엇인지는 별로 중요하지 않다. 알파벳 보드를 만들어서 만들어야 할 팀네임에 각 알파벳이 몇 번 등장했는지 파악하고, 팀원들의 이름의 첫 글자가 만들어야 할 팀네임 알파벳에 있다면 그것이 몇 번 등장했는지 세어준다.
첫 번째 예시
DPS의 경우 D가 1번, P가 1번, S가 1번 등장하고, 팀원들의 이름에는 D가 2번, P가 1번, S가 1번 등장한다. D로 시작하는 팀원이 2명이고, D를 1번 완성시켜야 하므로 경우의 수는 $_2C_1$이다. 마찬가지로 P는 $_1C_1$, S는 $_1C_1$이고, 답은 $_2C_1$ * $_1C_1$ * $_1C_1$로 2가 된다.다만 만들어야 할 팀네임에 있는 알파벳이 팀원들의 첫 글자에 없는 경우, 완성시킬 수가 없으므로 0을 출력하는 것으로 예외 처리한다.
$_nC_k$를 반환받는 함수를 작성하는 법은 재귀를 이용하는 법과, 동적 프로그래밍을 사용하는 방법이 있다. 두 방법 모두 본질적인 방법은 유사하다. 바로 $_nC_k = _{n-1} \mathrm C _{k-1} + _{n-1} \mathrm C _{k}$라는 점을 활용하는 것이다.
재귀를 사용하는 함수는 아래와 같다.
ll comb(int n, int k)
{
if (k == 0 || k == n)
return 1;
return comb(n - 1, k - 1) + comb(n - 1, k);
}
이 함수의 경우 들어올 수 있는 n과 k가 커서 그런지 재귀를 사용하면 시간 초과가 발생한다. 따라서 dp를 사용해서 메모이제이션을 해야 한다.
dp를 사용하는 방법은 아래와 같다.
ll comb(int n, int k)
{
ll dp[n + 1][k + 1];
for (int i = 0; i <= n; i++)
fill(dp[i], dp[i] + k, 0);
for (int i = 0; i <= n; i++) {
for (int j = 0; j <= min(i, k); j++) {
if (j == 0 || j == i) {
dp[i][j] = 1;
}
else {
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
}
}
}
return dp[n][k];
}
- 본질은 같지만 시간 복잡도가 dp가 훨씬 낮기 때문에 사용한다면 dp를 사용하는 것을 익혀두는 것이 좋겠다.
