BOJ 4883 - 삼각 그래프
“다이나믹 프로그래밍”
BOJ 4883 - 삼각 그래프
문제 링크

#include <bits/stdc++.h>
#include <cmath>
#define all(x) (x).begin(), (x).end()
#define rep(i, a, b) for (int i = (a); i < (b); ++i)
const int INF = 0x3f3f3f3f;
using namespace std;
int N;
int board[100010][4];
int dp[100010][4];
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL);
int test = 1;
while (1) {
cin >> N;
if (N == 0)
return 0;
for (int i = 0; i < N; i++) {
for (int j = 0; j < 3; j++)
cin >> board[i][j];
}
dp[0][0] = INF;
dp[0][1] = board[0][1];
dp[0][2] = dp[0][1] + board[0][2];
dp[1][0] = board[0][1] + board[1][0];
dp[1][1] = min({dp[1][0] + board[1][1], dp[0][1] + board[1][1], dp[0][2] + board[1][1]});
dp[1][2] = min({dp[1][1] + board[1][2], dp[0][1] + board[1][2], dp[0][2] + board[1][2]});
for (int i = 2; i < N; i++) {
dp[i][0] = min(dp[i - 1][0] + board[i][0], dp[i - 1][1] + board[i][0]);
dp[i][1] = min({dp[i][0] + board[i][1], dp[i - 1][0] + board[i][1],
dp[i - 1][1] + board[i][1], dp[i - 1][2] + board[i][1]});
dp[i][2] = min({dp[i][1] + board[i][2], dp[i - 1][1] + board[i][2],
dp[i - 1][2] + board[i][2]});
}
cout << test << ". " << dp[N - 1][1] << '\n';
test += 1;
}
return 0;
}
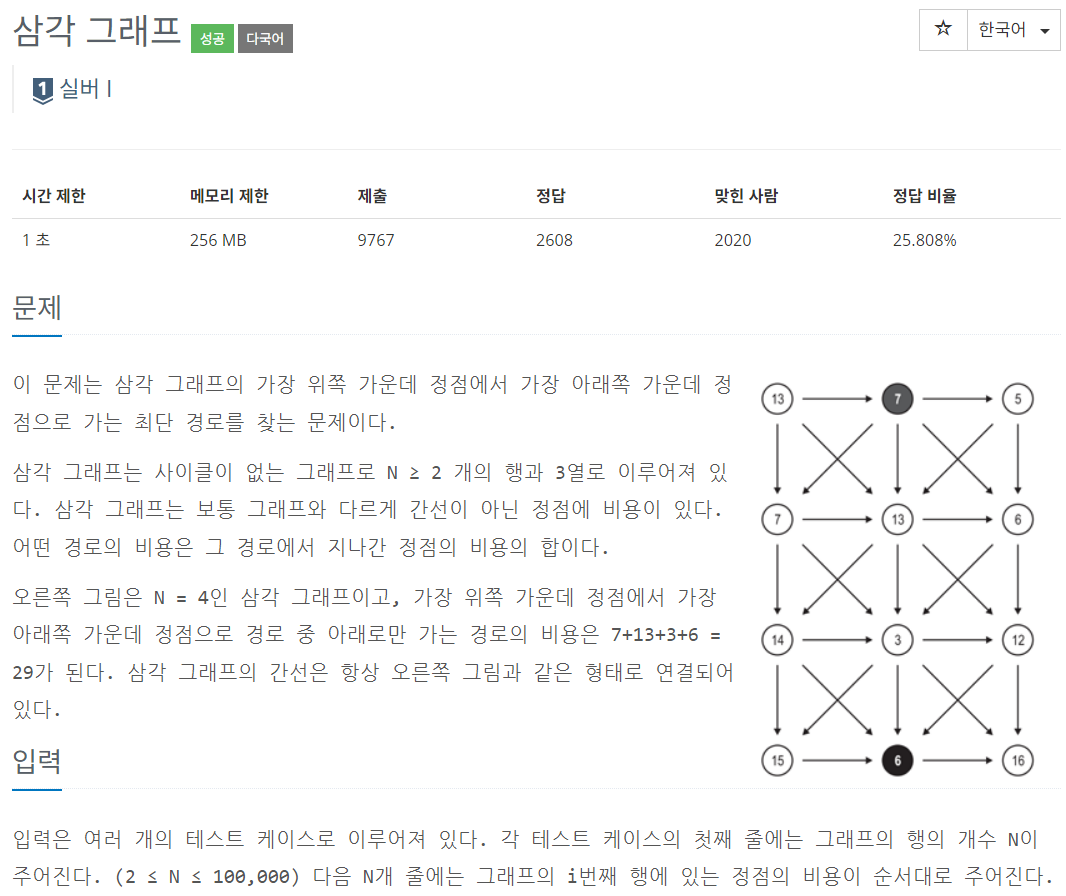
다이나믹 프로그래밍 문제를 좀 풀어봤다면, 꽤나 익숙한 스타일의 클래식한 dp 문제라는 걸 알 수 있다. 이 문제도 마찬가지로 출발점으로부터 그래프를 내려오면서 해당 node에서의 최댓값을 memoization 하고 특정 도착 지점의 최댓값을 출력하는 그런 문제다.
그러나 나는 그래프를 제대로 쳐다보지도 않고 머릿속에 박혀있는 풀이를 그대로 발사했다가 큰 낭패를 봤다. 그래프의 간선이 이동하는 방향을 잘 살펴봐야한다. 일반적인 문제처럼 위에서 아래로만 이동할 수 있는게 아니라, 같은 층의 노드에서도 움직일 수가 있다.
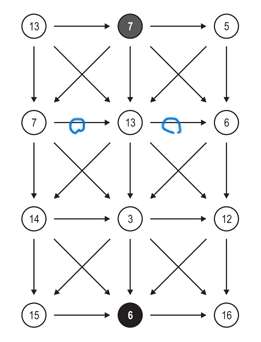
- 예를 들어서 2번째 행의 2번째 열 값인
13에 접근할 수 있는 경우의 수는 무엇이 있을까? 13에 접근하는 화살표의 수, 즉 4개이다.
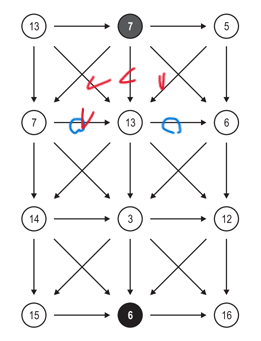
내가 알았던 유형에서는 저 파란 원 위에 있는 즉, 같은 층의 노드에서 접근하는 경우가 존재하지 않았고, 계속해서 저 경우를 제외하고 점화식을 세워서 WA를 받았었다…
첫 번째 행과 두 번째 행은 직접 경우를 작성했고, 그 아래 행부터는 점화식을 작성해서 풀었다. 첫 번째 행의 경우 첫 번째 행 첫 번째 값은 애초에 접근할 일이 없기 때문에 INF로 기록해두었다. 이후부터는 큰 틀에서 화살표의 수를 따져가며 경우를 작성하면 된다.
- 첫 번째 행
dp[0][0] = INF; // 거쳐갈 일이 없는 점 dp[0][1] = board[0][1]; // 시작점 dp[0][2] = dp[0][1] + board[0][2]; // 시작점에서 바로 옆으로 가는 화살표 단 하나 - 두 번째 행
// dp[0][0] 이 INF이기 때문에, 그쪽에서 내려오는 화살표를 고려할 필요는 없다. 첫 값의 경우 화살표 1개 dp[1][0] = board[0][1] + board[1][0]; // 가운데 값의 경우 화살표 3개 dp[1][1] = min({ dp[1][0] + board[1][1], dp[0][1] + board[1][1], dp[0][2] + board[1][1] }); // 끝 값의 경우 화살표 3개 dp[1][2] = min({ dp[1][1] + board[1][2], dp[0][1] + board[1][2], dp[0][2] + board[1][2] });
그 이외의 행
for (int i = 2; i < N; i++)
{
// 첫 값의 경우 화살표 2개
dp[i][0] = min(dp[i - 1][0] + board[i][0], dp[i - 1][1] + board[i][0]);
// 가운데 값의 경우 화살표 4개
dp[i][1] = min({
dp[i][0] + board[i][1],
dp[i - 1][0] + board[i][1],
dp[i - 1][1] + board[i][1],
dp[i - 1][2] + board[i][1]
});
// 끝 값의 경우 화살표 3개
dp[i][2] = min({
dp[i][1] + board[i][2],
dp[i - 1][1] + board[i][2],
dp[i - 1][2] + board[i][2]
});
}
