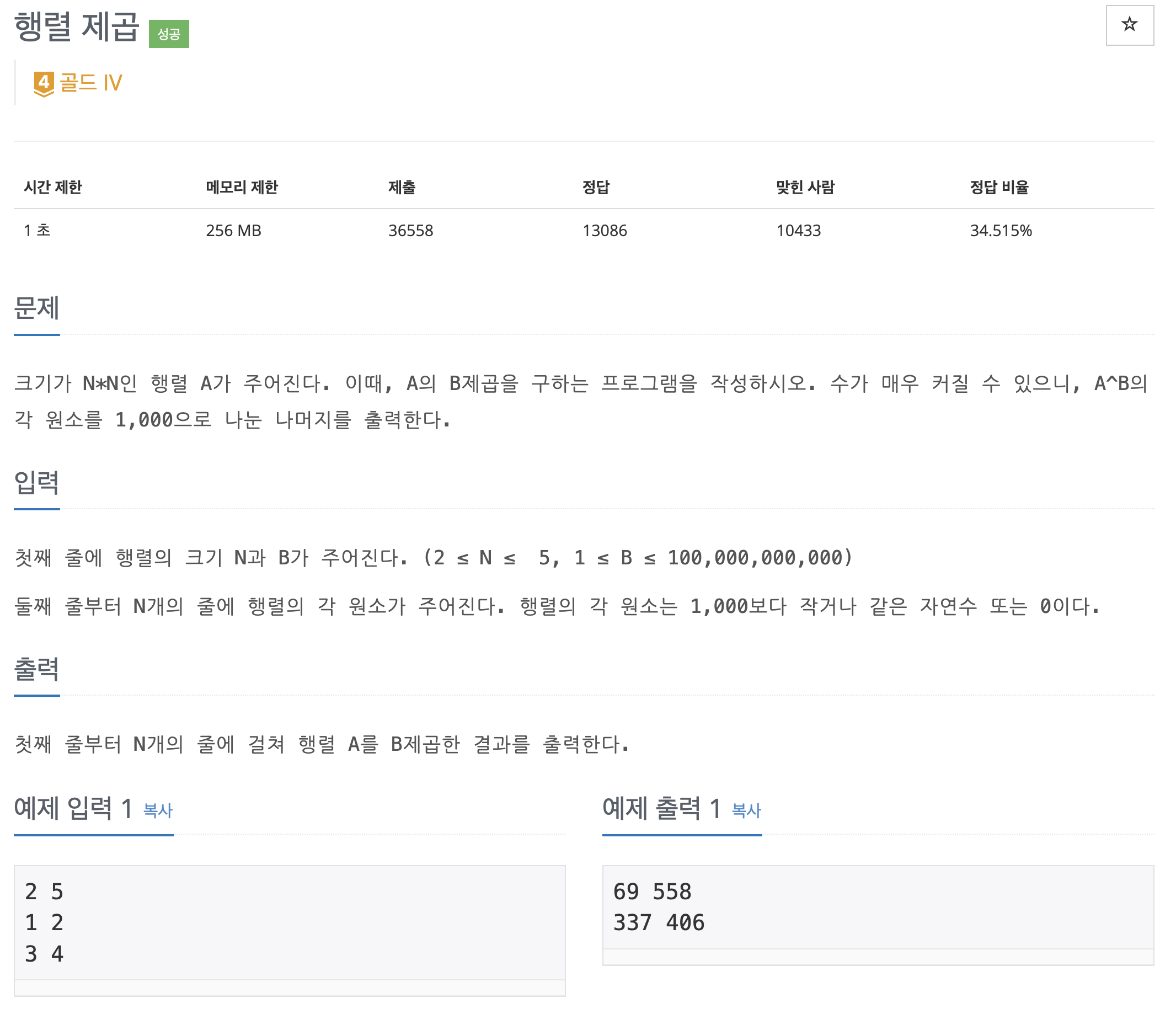
BOJ 10830 - 행렬 제곱

BOJ 10830 - 행렬 제곱

“단위 행렬, 행렬의 곱셈, 분할 정복”

BOJ 10830 - 행렬 제곱

문제 링크


#include <bits/stdc++.h>
typedef long long ll;
const int INF = 0x3f3f3f3f;
using namespace std;

int N;
ll B;
ll a[5][5]; // Input
ll tmp[5][5]; // 곱셈할때 쓸 임시배열
ll ans[5][5]; // 단위 행렬

void    Matrix_multi(ll x[5][5], ll y[5][5]) 
{
    for (int m = 0; m < N; m++) {
        for (int n = 0; n < N; n++) {
            tmp[m][n] = 0;
            for (int k = 0; k < N; k++) {
                tmp[m][n] += x[m][k] * y[k][n];
            }
            tmp[m][n] %= 1000;
        }
    }
    for (int i = 0; i < N; i++) {
        for (int j = 0; j < N; j++) {
            x[i][j] = tmp[i][j];
        }
    }
}

int main()
{
    ios_base::sync_with_stdio(false);
    cin.tie(NULL); cout.tie(NULL);

    cin >> N >> B;
    for (int i = 0; i < N; i++) {
        for (int j = 0; j < N; j++) {
            cin >> a[i][j]; // input 행렬 저장
        }
        ans[i][i] = 1; // 단위 행렬 입력
    }

    while (B > 0) {
        if (B % 2 == 1) {
            Matrix_multi(ans, a);
        }
        Matrix_multi(a, a);
        B /= 2;
    }

    for (int i = 0; i < N; i++) {
        for (int j = 0; j < N; j++) {
            cout << ans[i][j] << " ";
        }
        cout << '\n';
    }

    return 0;
}

  • 행렬을 제곱하기 위해 수학적 지식이 필요한 문제이다. 피보나치도 그렇고 이것도 그렇고 이런 문제들은 볼 때마다 답지를 보면서 죽을 쑤는데, 대부분 해당 문제에 관한 수학적 지식을 가지고 분할 정복을 이용하여 문제를 푸는 형태이다. 수학적 지식도 없는데 분할 정복도 잘 못하니 매번 쉽지 않은 경험을 하게 된다…

  • 행렬을 제곱하기 위해, 단위 행렬과 행렬의 곱셈을 알아야 한다.

Khan Academy, 단위행렬이란?

100
010
001


  • 단위 행렬은 주대각선의 원소가 모두 1이며 나머지 원소가 모두 0인 정사각 행렬이다. m * m 단위 행렬에 대해 아무 m * m 행렬을 곱해보면 자기 자신이 나온다는 것을 알 수 있다. 즉 단위 행렬은 곱셈의 항등원(1)과 같은 행렬이다. 제곱을 할 것이기 때문에 항등원 행렬을 준비해둘 필요가 있다.

  • 행렬의 곱셈의 경우, 행렬 A와 행렬 B를 곱한다고 했을 때 A의 열의 길이와 B의 행의 길이가 동일한 경우에만 곱셈이 행해질 수 있으며 결과로 나온 행렬은 A의 행의 길이 * B의 열의 길이의 크기를 가진다. 즉 A가 m * k 행렬이고 B가 k * n 행렬인 경우에만 곱셈 연산이 가능하며 결과로 나온 행렬은 m * n 크기의 행렬이다.

  • 두 행렬을 곱할 때, 반드시 A 행렬의 열 개수와 B 행렬의 행 개수가 동일해야 하는 이유는 행렬 A의 i번째 행과 행렬 B의 j번째 열의 성분을 순서대로 곱한 것이 행렬 AB의 (i, j)번째 성분이기 때문이다.


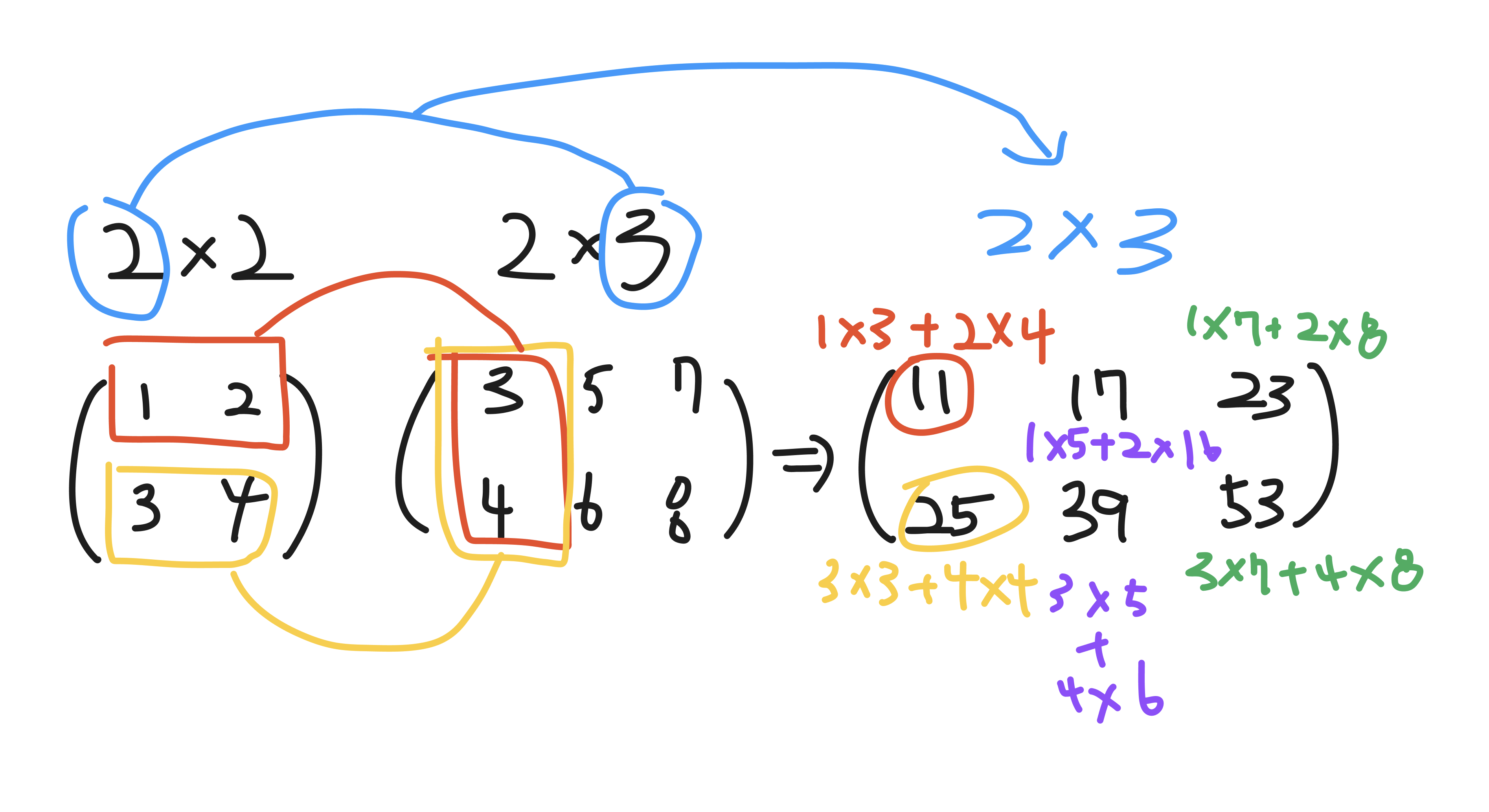
  • 예시로 그려본 행렬의 곱셈
void    Matrix_multi(ll x[5][5], ll y[5][5]) 
{
    for (int m = 0; m < N; m++) {
        for (int n = 0; n < N; n++) {
            tmp[m][n] = 0;
            for (int k = 0; k < N; k++) {
                tmp[m][n] += x[m][k] * y[k][n];
            }
            tmp[m][n] %= 1000;
        }
    }
    for (int i = 0; i < N; i++) {
        for (int j = 0; j < N; j++) {
            x[i][j] = tmp[i][j];
        }
    }
}
  • 그리고 이것이 행렬의 곱셈을 구현한 코드다. 행렬 A의 i번째 행과 행렬 B의 j번째 열의 성분을 순서대로 곱한 것이 행렬 AB의 (i, j)번째 성분 이라는 명제에 따라 구현된 것을 확인할 수 있다.
while (B > 0) {
    if (B % 2 == 1) {
        Matrix_multi(ans, a);
    }
    Matrix_multi(a, a);
    B /= 2;
}
  • 그리고 곱하는 횟수에 따라 분기를 나누는 반복문이다. 곱하는 횟수 B가 홀수라면 마지막에 한번 더 곱해줘야 하기 때문에 한번 더 곱해주는 코드를 써넣는다.