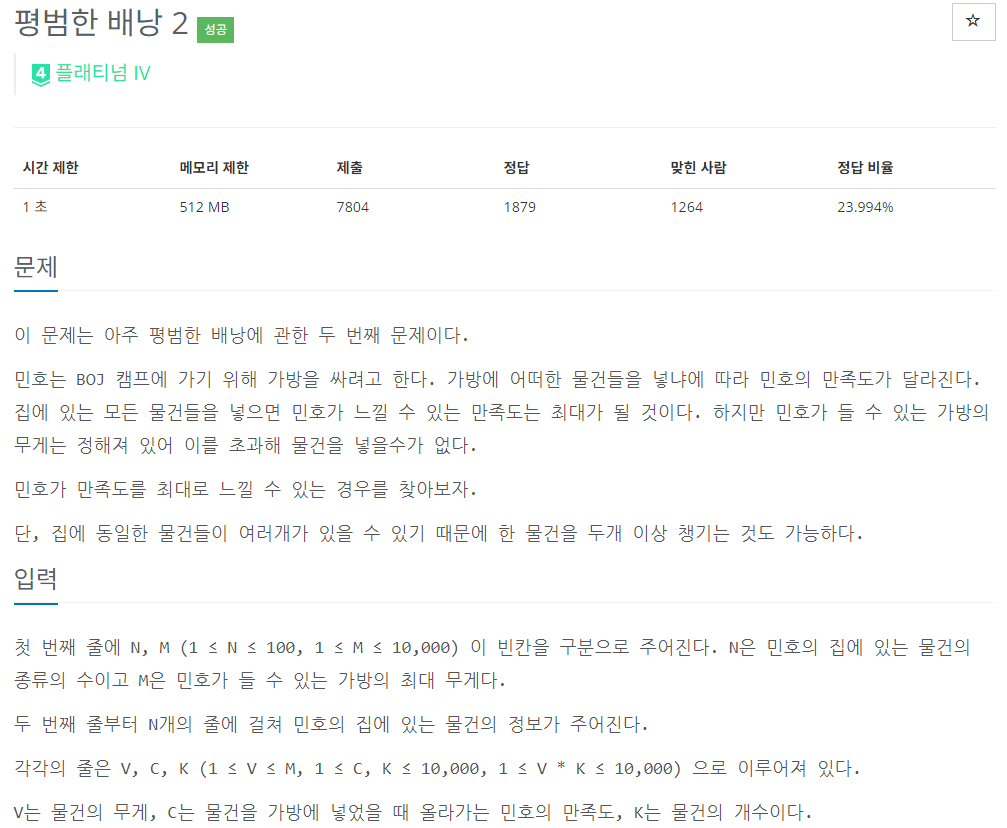
BOJ 12920 - 평범한 배낭 2
“배낭 문제”
문제 링크

CODE
#include <bits/stdc++.h>
#define all(x) (x).begin(), (x).end()
#define rep(i, a, b) for (int i = (a); i < (b); ++i)
const int INF = 0x3f3f3f3f;
using namespace std;
int N, M; // 물건갯수, 최대수용무게
int v[10101]; // 무게
int c[10101]; // 만족도
int k[10101]; // 개수
vector<pair<int,int>>vp;
int dp[1500][10101];
int W[10101];
int V[10101];
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL);
cin >> N >> M;
for (int i = 1; i <= N; i++)
cin >> v[i] >> c[i] >> k[i];
for (int i = 1; i <= N; i++) {
for (int j = k[i]; j >= 1; j >>= 1) {
int num = j - (j >> 1);
vp.push_back({v[i] * num, c[i] * num});
}
}
int nn = vp.size();
for (int i = 1; i <= nn; i++) {
W[i] = vp[i - 1].first;
V[i] = vp[i - 1].second;
}
for (int i = 1; i <= nn; i++) {
for (int j = 0; j <= M; j++) {
if (W[i] <= j)
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - W[i]] + V[i]);
else
dp[i][j] = dp[i - 1][j];
}
}
cout << dp[nn][M];
return 0;
}
DESCRIPTION
앞 문제 평범한 배낭(이하 배낭1)에서 이어지는 평범한 배낭 2(이하 배낭2)이다. 배낭1이 골드 5인데, 배낭2는 플래티넘 4로 온도 차이가 꽤 심하다고 할 수 있다. 무엇이 문제의 난이도를 가른 걸까?
배낭2는 같은 물건을 여러번 선택 가능한 배낭 문제의 변형이다. 배낭1의 풀이를 알고 있다면 배낭2도 같은 식으로 접근할 수가 있는데, 그렇게 접근하면 시간 초과가 난다. 배낭1의 풀이 방식은
int dp[물건의 갯수][수용 가능한 무게]의 이차원 정수 배열을 사용하는 것인데, 배낭2의 경우 MAX 물건의 개수가 100개에 수용 가능한 무게가 10000까지 들어오고(여기까지 시간 복잡도100 * 10000으로 안전) 거기다가 한 물건이 또 10000개까지 있을 수가 있기 때문에 실질적인 시간 복잡도가100 * 10000 * 10000으로,O(N * M * K)안전한 범위를 한참 넘어서게 된다. 이 때문에 별도의 최적화 논리를 필요로 한다.이 논리의 경우 구글 선생님의 도움을 좀 받았다. 보아하니 대중적으로 알려진 기법으로 보이는데, 바로 물건의 개수를 2의 제곱수로 분할하는 것이다. 이른바 이진 분할을 하는 것인데 물건의 수량을 이진수로 분해하고 분할된 물건을 마치 별도의 물건으로 처리하는 것이다.
예를 들어 물건의 개수가 13개라면, 이것을 x1, x2, x4, x6
(13 - (1 + 2 + 4))인 별도의 물건 4개로 분할하는 것이다. 이러면 물건 13개를 일일히 계산하지 않고도 모든 경우의 수를 확인할 수가 있다고 한다. 실제로 1 2 4 6을 이용해 1부터 13까지의 모든 수를 만들어볼 수가 있다. 이런식으로 최적화하면 물건의 개수 K가 \(\log_2 K\)로 떨어지게 되고 시간 복잡도는 O(100 * \(\log_2 10000\) * 10000)으로 사실상O(100 * 10000)과 동일한 시간 복잡도에 문제를 해결할 수가 있게 된다. 실제로 10000을 이진 분할하면 (\(\log_2 10000\)) 약 13(13.287...)이 된다.물건의 개수 K에 따라 이진 분할하는 코드는 아래와 같다. 이 코드도 나중에 써먹을 일이 있을 것 같기 때문에 숙지해두는 것이 좋을 것 같다. 비트 연산을 이용하여 깔끔하게 입력된 수를 이진 분할한다.
for (int i = 1; i <= N; i++) {
for (int j = k[i]; j >= 1; j >>= 1) {
int num = j - (j >> 1);
vp.push_back({v[i] * num, c[i] * num});
}
}
vector<pair<int,int>> vp는 새로이 정리한 물건의 배열로, 이 vp 배열을 구했다면 배낭1에서 사용한 방법 그대로 문제를 풀면 된다. 단 주의해야 할 점이 있다. 바로 이차원 배열dp[물건의 개수][무게]의 크기에 관한 것이다.무게의 경우 알다시피 10000이 한도이기 때문에 10000보다 조금 크게 설정하면 되지만 물건의 개수의 경우 vp가 만들어질 수 있는 최대의 경우를 고려하여 설정해야 한다. 처음에는
dp[110][10101]로 만들었다가 무수한 실패의 향연을 겪었다. vp의 최대 경우는 다음과 같다.물건 종류가 100개이고
(N = 100), 무게는 전부 1(V = 1), 개수는 10000개(K=10000)일때, 이진 분할 횟수는 \(\log_2 10000\) + 1로 약 14번이고, 물건의 종류가 100개이므로 vp의 size는 최소 1400개 이상으로 들어올 수가 있다. 따라서 이차원 배열dp[물건의 개수][무게]의 물건의 개수 칸을 넉넉하게 주지 않으면 outofbound 에러가 발생하게 되는 것이다.처참한 실험의 현장
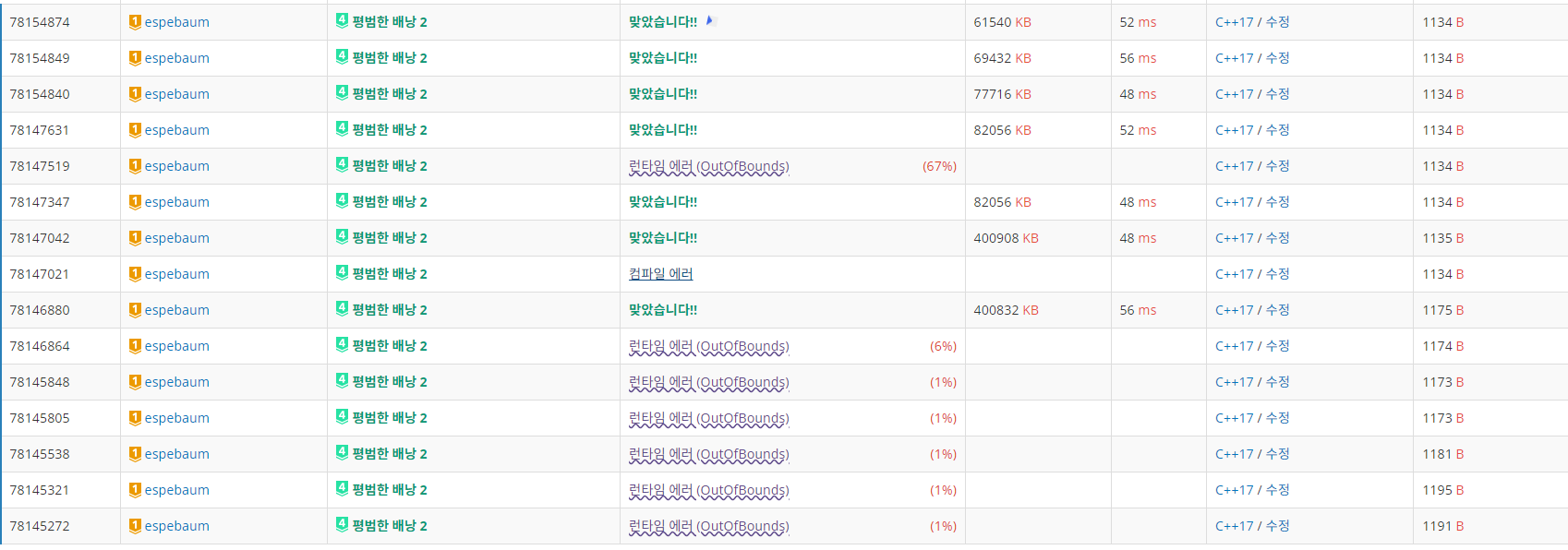
- vp 배열에 가치와 무게에 따라 새롭게 물건을 정렬한 이후에는 배낭1의 풀이를 그대로 가져와서 적용한다. 시간 복잡도를 최적화했기 때문에 무리없이 통과할 수가 있다.
int N, M; // 물건갯수, 최대수용무게
int v[10101]; // 무게
int c[10101]; // 만족도
int k[10101]; // 개수
vector<pair<int,int>>vp; // 새롭게 만든 물건 무게와 가치가 담긴 배열
int dp[1500][10101]; // 새로운 물건들로 채울 dp 배열
int W[10101]; // 새로운 물건들의 무게들
int V[10101]; // 새로운 물건들의 가치들
// ... 이전의 구현부
for (int i = 1; i <= nn; i++) {
W[i] = vp[i - 1].first;
V[i] = vp[i - 1].second;
}
// 배낭1의 로직을 그대로 사용
for (int i = 1; i <= nn; i++) {
for (int j = 0; j <= M; j++) {
if (W[i] <= j)
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - W[i]] + V[i]);
else
dp[i][j] = dp[i - 1][j];
}
}
cout << dp[nn][M];
return 0;
- 처음 손대본 플레티넘 문제였는데, 확실히 최적화가 쉽지 않다는 것을 체감했다.
