BOJ 13702 - 이상한 술집
문제 링크

CODE
#include <bits/stdc++.h>
#define all(x) (x).begin(), (x).end()
#define rep(i, a, b) for (int i = (a); i < (b); ++i)
typedef long long ll;
const int INF = 0x3f3f3f3f;
using namespace std;
ll N, K; // 주전자의 개수(N), 친구들의 수(K)
ll arr[10101];
bool solve(int x) // 결정 함수
{
int cur = 0;
for (int i = 0; i < N; i++)
cur += arr[i] / x;
return cur >= K;
}
signed main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL); std::cout.tie(NULL);
cin >> N >> K;
for (int i = 0; i < N; i++)
cin >> arr[i];
ll st = 0;
ll en = pow(2, 31) - 1;
while (st < en)
{
ll mid = (st + en + 1) / 2; // 매개 변수
if (solve(mid))
st = mid;
else
en = mid - 1;
}
cout << st;
return 0;
}
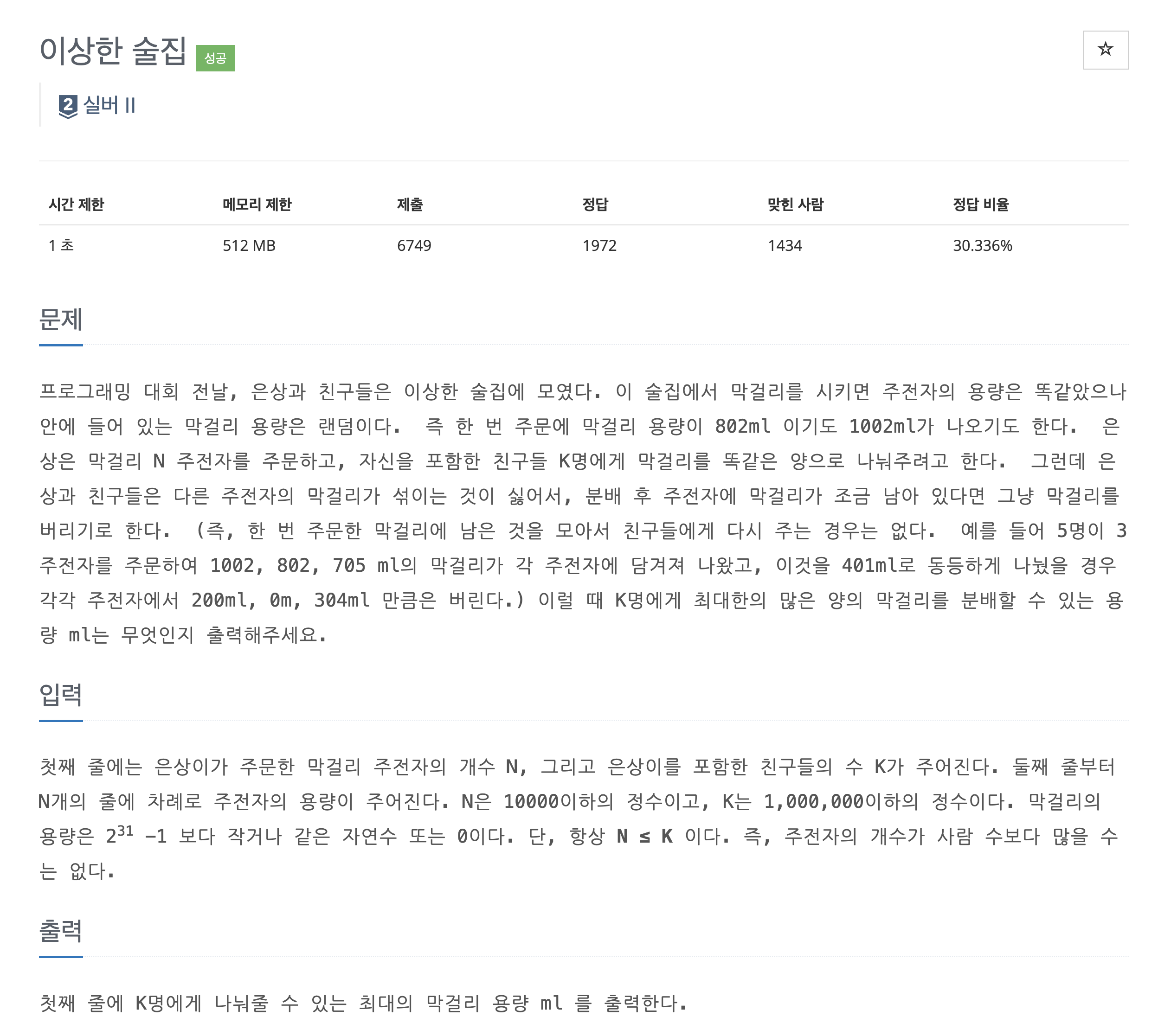
DESCRIPTION
매개 변수 탐색을 사용해야 하는 문제이다. 이분 탐색과 매커니즘은 동일하다. 이분 탐색이 정렬된 배열이나 리스트에서 특정 값을 찾는데 사용된다면, 매개 변수 탐색은 특정 조건을 만족하는 최적해를 찾는 것에 사용된다고 볼 수 있다.
일반 이분 탐색이 중앙값을 구하여(예를 들어
mid = st + en / 2) 해당 중앙 값이 찾는 값보다 큰 지, 작은 지 혹은 같은 지를 파악한다면 매개 변수 탐색은 중앙값이 문제의 조건을 만족하는지를 판단한다.즉 매개 변수 탐색은 매개 변수와 결정 함수로 구성된다. 이것은 나무 자르기나 랜선 자르기같은 매개 변수 탐색을 사용하는 문제라면 똑같이 적용할 수 있다. 매개 변수는 중앙값이고, 결정 함수는 그 중앙값이 문제의 조건, K명에게 최대한 많은 양의 막걸리를 분배할 수 있느냐가 되겠다.
solve()함수는 보다시피 매개 변수로 받은 막걸리의 양만큼 실제 주전자에서 친구들에게 막걸리를 분배하면서 그 수가 친구들의 수만큼 나오는지를 확인해보는 결정 함수이다. 매개변수가 최적해보다 크다면 모든 친구들에게 막걸리를 나눠 줄 수 없을 것이고, 작다면 최대의 막걸리를 나눠줄 수 없을 것이다.조건을 만족하는 최적해는 st와 en이 같을 때 등장하게 된다. 최적해를 찾으면 이분 탐색은 종료된다.
