BOJ 2166 - 다각형의 면적

19 Feb 2024 in Posts on Random, CPP

“신발끈 공식으로 N각형 넓이 구하기”

• BOJ 2166 - 다각형의 면적
  • 문제 링크

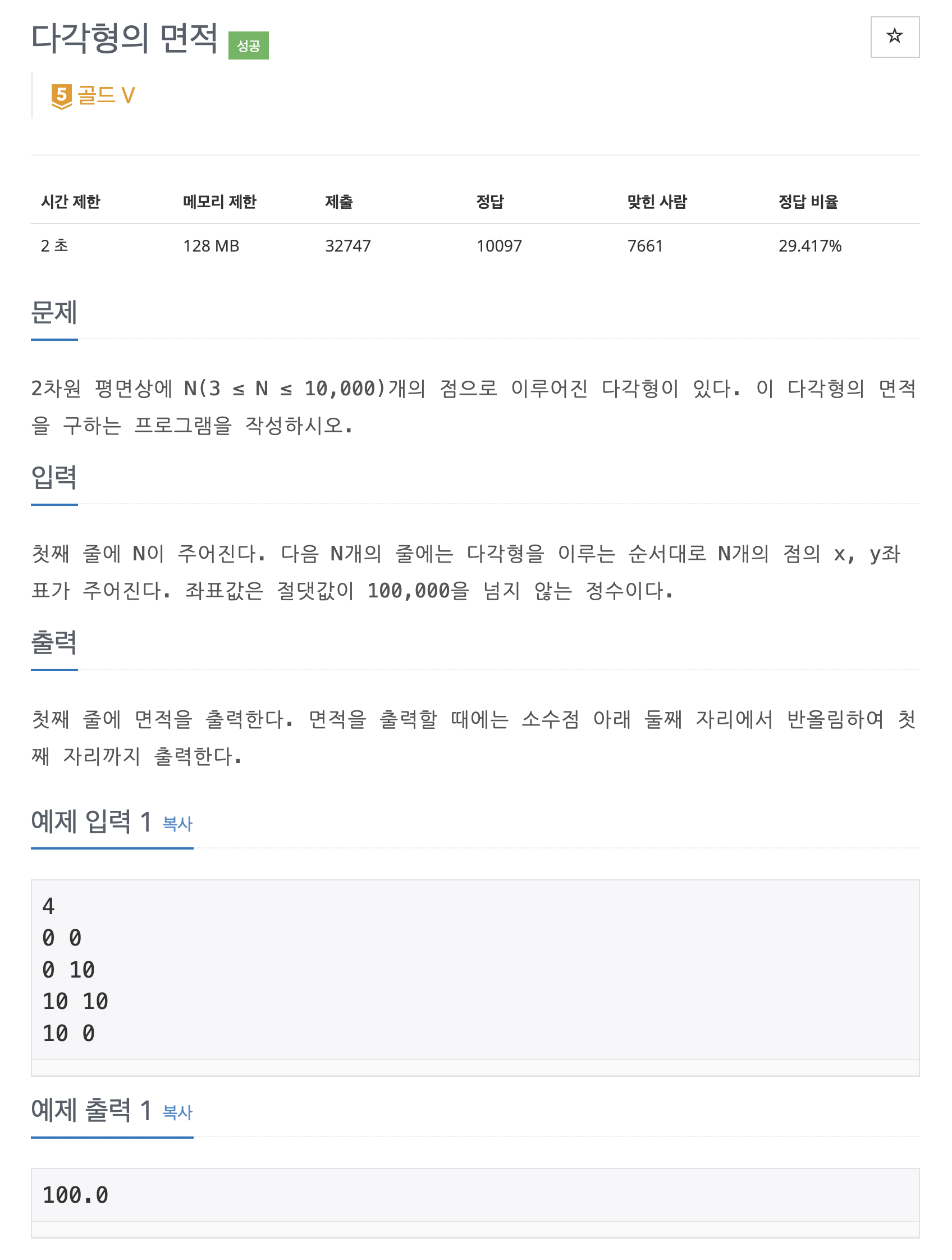
BOJ 2166 - 다각형의 면적

문제 링크

#include <bits/stdc++.h>
typedef long long ll;
const int INF = 0x3f3f3f3f;
using namespace std;

int N;
vector<pair<double,double>>vp;

void    check()
{
    double first = 0;
    for (int i = 0; i < N; i++) {
        if (i+1 == N)
            first += (double)vp[i].first*vp[0].second;
        else
            first += (double)vp[i].first*vp[i+1].second;
    }
    double second = 0;
    for (int i = 0; i < N; i++) {
        if (i+1 == N)
            second += (double)vp[0].first*vp[i].second;
        else
            second += (double)vp[i+1].first*vp[i].second;
    }
    double res = abs(first - second) * 0.5;
    cout << fixed << setprecision(1) << res; 
}

int main()
{
    ios_base::sync_with_stdio(false);
    cin.tie(NULL); cout.tie(NULL);
    cin >> N;
    for (int i = 0; i < N; i++) {
        double x,y; cin>>x>>y;
        vp.push_back({x,y});
    } 
    check();
    return 0;
}

• 바로 이전 포스트인 CCW와 결이 같은 문제이다. 신발끈 공식의 강력함을 깨달을 수 있었다. 어떠한 N각형의 넓이라도 구할 수 있다.

• <iomanip> 헤더를 사용하면, 고정 소수 표기를 지원하는 std::fixed와 정밀도를 설정할 수 있는 std::setprecision을 사용할 수 있다. 좋은 기능이긴 한데, <bits/stdc++.h> 헤더를 사용할 수 있다면 그냥 쓸 수 있기도 하다.